Page 305 - Becoming Metric Wise

297
The Informetric Laws

Note that (logically!) t 0 . 0as0 , a , 1. Moreover, t 0 does not
dependent on the type of logarithm used to perform the calculation.

9.2.3 Growth

At first sight, it seems that the growth of the literature has nothing to do
with obsolescence. Yet, already many years ago Brookes (1970) wrote that
the methodology to study these two phenomena is the same.
One may study yearly growth, comparing occurrences in one year
with occurrences during the next one, or cumulative growth. The meth-
odology is again essentially the same. The simplest, and most used,
growth curve is exponential growth. If g(t) denotes the number of docu-
ments in year t, then exponential growth is expressed as:
gtðÞ 5 ga t (9.4)
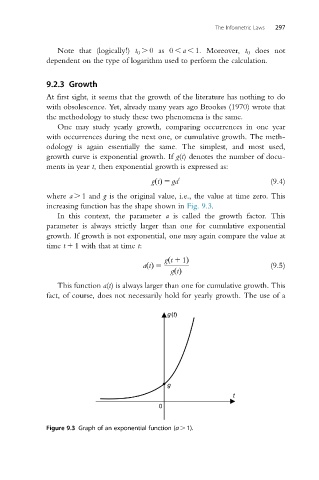
where a . 1 and g is the original value, i.e., the value at time zero. This
increasing function has the shape shown in Fig. 9.3.
In this context, the parameter a is called the growth factor. This
parameter is always strictly larger than one for cumulative exponential
growth. If growth is not exponential, one may again compare the value at
time t 1 1 with that at time t:

gt 1 1Þ
ð
atðÞ 5 (9.5)
gtðÞ
This function a(t) is always larger than one for cumulative growth. This
fact, of course, does not necessarily hold for yearly growth. The use of a

Figure 9.3 Graph of an exponential function (a . 1).