Page 201 - Biaxial Multiaxial Fatigue and Fracture

Estimation of the Fatigue Life of High Strength Steel Under ... 185

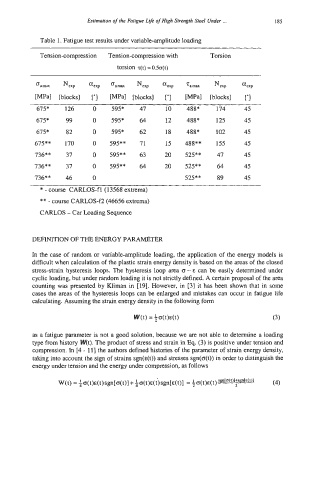
Table 1. Fatigue test results under variable-amplitude loading

Tension-compression Tension-compression with Torsion
torsion qt) = O.%(t)

damax Nexp aexp dam Nap aexp ramax Nexp aexp
[blocks] ["I [MPal [blocks] ['I [MPal [blocks] ['I
675* 126 0 595* 47 10 488* 174 45
675* 99 0 595* 64 12 488" 125 45
675* 82 0 595* 62 18 488" 102 45
675** 170 0 595** 71 15 488** 155 45
736** 37 0 595** 63 20 525** 47 45
736** 37 0 595** 64 20 525** 64 45
136** 46 0 525** 89 45
* - course CARLOS-fl (13568 extrema)
** - course CARLOSf2 (46656 extrema)

CARLOS - Car Loading Sequence

DEFINlTION OF THE ENERGY PARAMETER

In the case of random or variable-amplitude loading, the application of the energy models is
difficult when calculation of the plastic strain energy density is based on the areas of the closed
stress-strain hysteresis loops. The hysteresis loop area a - E can be easily determined under
cyclic loading, but under random loading it is not strictly defined. A certain proposal of the area
counting was presented by Kliman in [19]. However, in 131 it has been shown that in some
cases the areas of the hysteresis loops can be enlarged and mistakes can occur in fatigue life
calculating. Assuming the strain energy density in the following form

as a fatigue parameter is not a good solution, because we are not able to determine a loading
type from history W(t). The product of stress and strain in J3q. (3) is positive under tension and
compression. In [4 - 111 the authors defined histories of the parameter of strain energy density,
taking into account the sign of strains sgn(e(t)) and stresses sgn(a(t)) in order to distinguish the
energy under tension and the energy under compression, as follows