Page 178 - Buried Pipe Design

152 Chapter Three

(s – s )
3 ult
1
s = Maximum Principal Stress
1
s = Minimum Principal Stress
3
(s 1 – s 3 ) E i 1 e = Strain
(s – s ) = Ultimate Soil Strength
1
3 ult
Real
e
(s – s ) = e
3
1
1 + e
E i (σ – σ )
3 ult
1
1
3 ult
1
e s 1 – s 3 1 (s – s ) Transformed
e = 1 + e
1 (s – s ) E i (s – s )
1
1
3 ult
3
E i
e
Figure 3.38 Hyperbolic presentation of a stress-strain curve. (After
Duncan et al. 6 )
available strength is mobilized), the value of the modulus of elasticity
approaches zero.
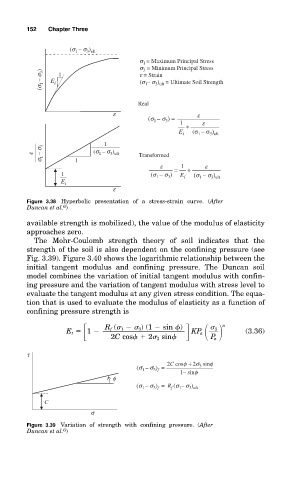
The Mohr-Coulomb strength theory of soil indicates that the
strength of the soil is also dependent on the confining pressure (see
Fig. 3.39). Figure 3.40 shows the logarithmic relationship between the
initial tangent modulus and confining pressure. The Duncan soil
model combines the variation of initial tangent modulus with confin-
ing pressure and the variation of tangent modulus with stress level to
evaluate the tangent modulus at any given stress condition. The equa-
tion that is used to evaluate the modulus of elasticity as a function of
confining pressure strength is
R f (
1
3 ) (1 sin
) n

3
E t 1 KP a (3.36)
2C cos
2
3 sin
P a
t
2C cosf +
(s – s ) = 2s 3 sinf
1
3 f
1– sinf
f
(s – s ) = R (s – s )
1
1
3 ult
f
3 f
C
s
Figure 3.39 Variation of strength with confining pressure. (After
Duncan et al. 6 )