Page 141 - Carbon Nanotubes

Vibrational modes of carbon nanotubes 131
allowed r-point vibrations for graphite (3D) are shown
in Fig. Id, which consist of two, doubly degenerate,
Raman-active modes (E;;) at 42 cm-', E;:' at 1582
cm-I), a doubly degenerate, infrared-active El , mode
at 1588 cm-' , a nondegenerate, infrared-active AZu
mode at 868 cm-', and two doubly degenerate Bzg
modes (127 cm-', 870 cm-') that are neither Raman-
nor infrared-active. The lower frequency Bii) mode
has been observed by neutron scattering, and the other
is predicted at 870 cm-'. Note the I'-point El, and
15;;) modes have the same intralayer motion, but dif-
fer in the relative phase of their C-atom displacements
in adjacent layers. Thus, it is seen that the interlayer
interaction in graphite induces only an -6 cm-' split-
(2)
ting between these modes (w(El,) - @(Ez, ) = 6
cm-')). Furthermore, the frequency of the rigid-layer,
shear mode (o(E2;)) = 42 cm-') provides a second
spectroscopic measure of the interlayer interaction be-
cause, in the limit of zero interlayer coupling, we must
have w (E;:) ) + 0.
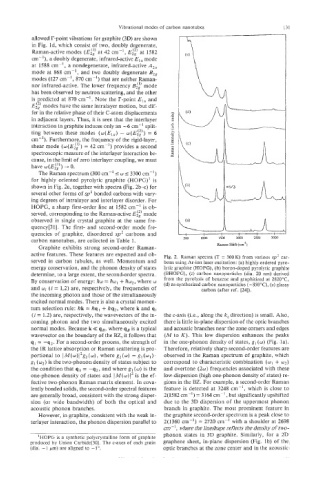
The Raman spectrum (300 cm-' I I 3300 cm-')
w
for highly oriented pyrolytic graphite (HOPG)' is
shown in Fig. 2a, together with spectra (Fig. 2b-e) for
several other forms of sp2 bonded carbons with vary-
ing degrees of intralayer and interlayer disorder. For
HOPG, a sharp first-order line at 1582 cm-' is ob-
served, corresponding to the Raman-active E;:) mode
observed in single crystal graphite at the same fre-
quency[3 I]. The first- and second-order mode fre-
quencies of graphite, disordered sp2 carbons and
carbon nanotubes, are collected in Table 1.
Graphite exhibits strong second-order Raman-
active features. These features are expected and ob- Fig. 2. Raman spectra (T = 300 K) from various sp2 car-
served in carbon tubules, as well. Momentum and bons using Ar-ion laser excitation: (a) highly ordered pyro-
energy conservation, and the phonon density of states lytic graphite (HOPG), (b) boron-doped pyrolytic graphite
determine, to a large extent, the second-order spectra. (BHOPG), (c) carbon nanoparticles (dia. 20 nm) derived
from the pyrolysis of benzene and graphitized at 282OoC,
By conservation of energy: Aw = Awl + hw,, where o (d) as-synthesized carbon nanoparticles (-85OoC), (e) glassy
and wi (i = 1,2) are, respectively, the frequencies of carbon (after ref. [24]).
the incoming photon and those of the simultaneously
excited normal modes. There is also a crystal momen-
tum selection rule: hk = Aq, + Aq,, where k and qi
(i = 1.2) are, respectively, the wavevectors of the in- the c-axis (i.e., along the k, direction) is small. Also,
coming photon and the two simultaneously excited there is little in-plane dispersion of the optic branches
normal modes. Because k << qe, where qB is a typical and acoustic branches near the zone corners and edges
wavevector on the boundary of the BZ, it follows that (M to K). This low dispersion enhances the peaks
ql = -q2. For a second-order process, the strength of in the one-phonon density of states, g, (w) (Fig. la).
the IR lattice absorption or Raman scattering is pro- Therefore, relatively sharp second-order features are
portional to IM(w)12g2(o), where g2(w) = gl(wl). observed in the Raman spectrum of graphite, which
g, (a,) is the two-phonon density of states subject to correspond to characteristic combination (wl + w2)
the condition that q1 = -q2, and where g, (w) is the and overtone (2w) frequencies associated with these
one-phonon density of states and IM(w)I2 is the ef- low-dispersion (high one-phonon density of states) re-
fective two-phonon Raman matrix element. In cova- gions in the BZ. For example, a second-order Raman
lently bonded solids, the second-order spectra1 features feature is detected at 3248 cm-', which is close to
are generally broad, consistent with the strong disper- 2(1582 cm-') = 3164 cm-', but significantly upshifted
sion (or wide bandwidth) of both the optical and due to the 3D dispersion of the uppermost phonon
acoustic phonon branches. branch in graphite. The most prominent feature in
However, in graphite, consistent with the weak in- the graphite second-order spectrum is a peak close to
terlayer interaction, the phonon dispersion parallel to 2(1360 cm-') = 2720 cm-' with a shoulder at 2698
cm-' , where the lineshape reflects the density of two-
'HOPG is a synthetic polycrystalline form of graphite phonon states in 3D graphite. Similarly, for a 2D
produced by Union Carbide[30]. The c-axes of each grain graphene sheet, in-plane dispersion (Fig. Ib) of the
(dia; -1 pm) are aligned to -1". optic branches at the zone center and in the acoustic