Page 136 - Carbon Nanotubes

126 J.-P. ISSI et al.
measurements on individual single-wall well-charac-
terized tubes have not been published to date. Exper- 0.0
iments usually involve gathering nanotube material -
from several growths, to obtain quantities of material (r
on the order of tens of mg. A measurement on ori- \-0.2
2
ented bundles of tubes[30] at 0.5 T as a function of E
a,
temperature gives evidence for anisotropy. Such a "-0.4
measurement is, however, easily affected by a small CI
c
misalignment of the sample. It is, therefore, possible a
that the data reported for the case where the field is E -0.6
0
parallel to the tube axis are, in fact, dominated by con- r
tributions from the perpendicular susceptibility. -0.8
A second study [33] on samples that contain a mix-
ture of nanotubes, together with several percent
"buckyonion"-type structures, was carried out at tem- -1 .o 0 20000 40000 60000
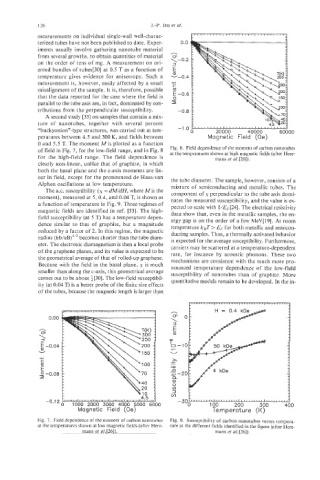
peratures between 4.5 and 300 K, and fields between Magnetic Field (Oe)
0 and 5.5 T. The moment Mis plotted as a function
of field in Fig. 7, for the low-field range, and in Fig. 8 Fig. 8. Field dependence of the moment of carbon nanotubes
at the temperatures shown at high magnetic fields (after Here-
for the high-field range. The field dependence is mans et al. [26]).
clearly non-linear, unlike that of graphite, in which
both the basal plane and the c-axis moments are lin-
ear in field, except for the pronounced de Haas-van the tube diameter. The sample, however, consists of a
Alphen oscillations at low temperature. mixture of semiconducting and metallic tubes. The
The a.c. susceptibility (x = dM/dH, where Mis the component of x perpendicular to the tube axis domi-
moment), measured at 5,0.4, and 0.04 T, is shown as nates the measured susceptibility, and the value is ex-
a function of temperature in Fig. 9. Three regimes of pected to scale with 1/EF[24]. The electrical resistivity
magnetic fields are identified in ref. [33]. The high- data show that, even in the metallic samples, the en-
field susceptibility (at 5 T) has a temperature depen- ergy gap is on the order of a few MeV[19]. At room
dence similar to that of graphite, but a magnitude temperature kBT > EF for both metallic and semicon-
reduced by a factor of 2. In this regime, the magnetic ducting samples. Thus, a thermally activated behavior
radius (hb/eB)"' becomes shorter than the tube diam- is expected for the average susceptibility. Furthermore,
eter. The electronic diamagnetism is then a local probe carriers may be scattered at a temperature-dependent
of the graphene planes, and its value is expected to be rate, for instance by acoustic phonons. These two
the geometrical average of that of rolled-up graphene. mechanisms are consistent with the much more pro-
Because with the field in the basal plane, x is much nounced temperature dependence of the low-field
smaller than along the c-axis, this geometrical average susceptibility of nanotubes than of graphite. More
comes out to be about +[30]. The low-field susceptibil- quantitative models remain to be developed. In the in-
ity (at 0.04 T) is a better probe of the finite size effects
of the tubes, because the magnetic length is larger than

L' ' " ' " " '" ' " " I ' " ' " '"# " ' " " '4
'
'
'
0.00
m
>
cn
E -0.04
a,
W
4
S
?
4 -0.08

4.5
-0.12
0 1000 2000 3000 4000 5000 6000
Magnetic Field (Oe)
Fig. 7. Field dependence of the moment of carbon nanotubes Fig. 9. Susceptibility of carbon nanotubes versus tempera-
at the temperatures shown at low magnetic fields (after Here- ture at the different fields identified in the figure (after Here-
mans et al.[26]). mans el a/. [26]).