Page 135 - Carbon Nanotubes

Electronic properties of carbon nanotubes 125
where Ef is the Fermi energy and A is the band over- these results are not consistent with WL. In the frame-
lap. C, and C, are the fitting parameters. The results work of WL, the observed temperature independent
of this fit, which is shown in Fig. 5, is obtained for MR below 10 K and down to 1 K could only be ex-
A = 3.7 MeV and with the Fermi energy right in the plained in the presence of large amounts of magnetic
middle of the overlap. Ideally, an overlap of the or- impurities, as is the case for some pyrocarbons[25].
der of 40 MeV is expected for the case of multilayered However, in the present case, the spectrographic anal-
nanotubes[23] with an interlayer configuration simi- ysis performed by Heremans et al. [26] excludes the
lar to that of crystalline graphite. For real nanotubes presence of magnetic impurities.
instead, a turbostratic stacking of the adjacent layers Below 2 K, an unexpected temperature dependence
would reduce drastically the interlayer interactions, as of the resistance and MR is observed. As shown in
in disordered graphite, and so it is not surprising to Fig. 5, the resistance presents, after an initial increase,
find a band overlap 10 times smaller than in crystalline a saturation or a broad maximum and an unexplained
graphite. This implies also that, within the frame of sharp drop when a magnetic field is applied (see Fig. 6).
the STB model, the carrier density is 10 times smaller. Further theoretical work is needed to get a better un-
The apparent electrical resistivity (4 x Om) mea- derstanding of these striking physical observations. Fi-
sured at low temperature is certainly still higher than nally, it is interesting to note that Whitesides and
the resistivity of a single nanotube. In fact, the con- Weisbecker[27] developed a technique to estimate the
ductance of the system is dominated by that of the conductivity of single nanotubes by dispersing nano-
nanotubes with the highest conductance (Le., the semi- tubes onto lithographically defined gold contacts to re-
metallic nanotubes). All these nanotubes are not nec- alize a 'nano-wire' circuit. From this 2-point resistance
essarily in contact with the measuring probes. Finally, measurement and, after measuring the diameter of the
the inner structure of each individual nanotube in this single nanotubes by non-contact AFM, they estimated
microbundle remains unknown. the room-temperature electrical resistivity along the
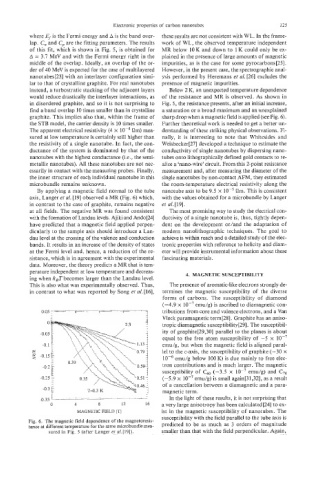
By applying a magnetic field normal to the tube nanotube axis to be 9.5 x low5 Qm. This is consistent
axis, Langer et ai. I191 observed a MR (Fig. 6) which, with the values obtained for a microbundle by Langer
in contrast to the case of graphite, remains negative et a/. 1191.
at all fields. The negative MR was found consistent The most promising way to study the electrical con-
with the formation of Landau levels. Ajiki and Ando[24] ductivity of a single nanotube is, thus, tightly depen-
have predicted that a magnetic field applied perpen- dent on the development or/and the adaptation of
dicularly to the sample axis should introduce a Lan- modern nanolithographic techniques. The goal to
dau level at the crossing of the valence and conduction achieve is within reach and a detailed study of the elec-
bands. It results in an increase of the density of states tronic properties with reference to helicity and diam-
at the Fermi level and, hence, a reduction of the re- eter will provide instrumental information about these
sistance, which is in agreement with the experimental fascinating materials.
data. Moreover, the theory predicts a MR that is tem-
perature independent at low temperature and decreas-
ing when kBT becomes larger than the Landau level. 4. MAGNETIC SUSCEPTIBILITY
This is also what was experimentally observed. Thus, The presence of aromatic-like electrons strongly de-
in contrast to what was reported by Song et a/. [16], termines the magnetic susceptibility of the diverse
forms of carbons. The susceptibility of diamond
(-4.9 x emu/g) is ascribed to diamagnetic con-
tributions from core and valence electrons, and a Van
Vleck paramagnetic term[28]. Graphite has an aniso-
tropic diamagnetic susceptibility[29]. The susceptibil-
ity of graphite[29,30] parallel to the planes is about
equal to the free atom susceptibility of -5 x
emu/g, but when the magnetic field is aligned paral-
lel to the c-axis, the susceptibility of graphite (-30 X
lop6 emu/g below loOK) is due mainly to free elec-
tron contributions and is much larger. The magnetic
susceptibility of C60 (-3.5 x emulg) and C70
(-5.9 x 10-~ emu/g) is small again[31,32], as a result
of a cancellation between a diamagnetic and a para-
-0.35 ' I magnetic term.
In the light of these results, it is not surprising that
0 ' ' 4 ' 8 12 16 a very large anisotropy has been calculated[24] to ex-
MAGNETIC FIELD [TI ist in the magnetic susceptibility of nanotubes. The
susceptibility with the field parallel to the tube axis is
Fig. 6. The magnetic field dependence of the magnetoresis-
tance at different temperature for the same microbundle mea- predicted to be as much as 3 orders of magnitude
sured in Fig. 5 (after Langer et n1.[19]). smaller than that with the field perpendicular. Again,