Page 51 - Carbon Nanotubes

42 J. W. MINTMIRE and C. T. WHITE

t i

0
0 0.5 1 1.5
Nanotube radius (nm)
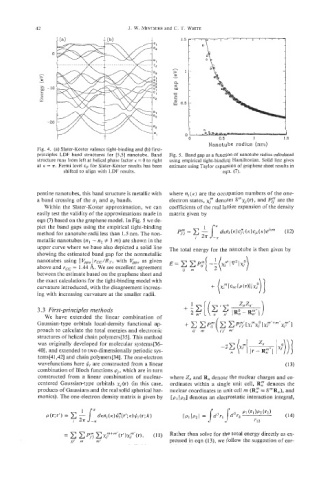
Fig. 4. (a) Slater-Koster valence tight-binding and (b) first-
principles LDF band structures for [5,5] nanotube. Band Fig. 5. Band gap as a function of nanotube radius calculated
structure runs from left at helical phase factor K = 0 to right using empirical tight-binding Hamiltonian. Solid line gives
at K = n. Fermi level E~ for Slater-Koster results has been estimate using Taylor expansion of graphene sheet results in
shifted to align with LDF results. eqn. (7).

pentine nanotubes, this band structure is metallic with where ni(K) are the occupation numbers of the one-
a band crossing of the a, and a2 bands. electron states, xj” denotes Srnxj(r), and Pf are the
Within the Slater-Koster approximation, we can coefficients of the real lattice expansion of the density
easily test the validity of the approximations made in matrix given by
eqn (7) based on the graphene model. In Fig. 5 we de-
pict the band gaps using the empirical tight-binding
method for nanotube radii less than 1.5 nm. The non-
metallic nanotubes (nl - n2 # 3 rn) are shown in the
upper curve where we have also depicted a solid line The total energy for the nanotube is then given by
showing the estimated band gap for the nonmetallic
nanotubes using I GpX) rcc/Rr, with V,, as given
above and rcc = 1.44 A. We see excellent agreement
between the estimate based on the graphene sheet and
the exact calculations for the tight-binding model with
curvature introduced, with the disagreement increas-
ing with increasing curvature at the smaller radii.

3.3 First-principles methods
We have extended the linear combination of
Gaussian-type orbitals local-density functional ap-
proach to calculate the total energies and electronic
structures of helical chain polymers[35]. This method
was originally developed for molecular systems[36-
401, and extended to two-dimensionally periodic sys-
tems[41,42] and chain polymers[34]. The one-electron
wavefunctions here J.i are constructed from a linear (13)
combination of Bloch functions pj, which are in turn
constructed from a linear combination of nuclear- where Z,, and R, denote the nuclear charges and co-
centered Gaussian-type orbitals xj (r) (in this case, ordinates within a single unit cell, Rr denotes the
products of Gaussians and the real solid spherical har- nuclear coordinates in unit cell rn (RZ = SmR,), and
monics). The one-electron density matrix is given by [ p1 I p2] denotes an electrostatic interaction integral,

Rather than solve for the total energy directly as ex-
pressed in eqn (13), we follow the suggestion of ear-