Page 52 - Carbon Nanotubes

Electronic and structural properties of carbon nanotubes 43
lier workers to fit the exchange-correlation 'potential
and the charge density (in the Coulomb potential) to
a linear combination of Gaussian-type functions.
We have carried out a series of geometry optimi- where E is the elastic modulus, R is the radius of cur-
zations on nanotubes with diameters less than 2 nm. vature, L is the length of the cylinder, and a is a rep-
We will present some results for a selected subset of resentative thickness of the order of the graphite
the moderate band gap nanotubes, and then focus on interplanar spacing (3.35 A). Assuming that the total
results for an example chiral systems: the chiral [9,2] number of carbons is given by N = 23rRL/hl, where
nanotube with a diameter of 0.8 nm. This nanotube hl is the area per carbon, we find that the strain energy
has been chosen because its diameter corresponds to per carbon is expected to be
those found in relatively large amounts by Iijima[7]
after the synthesis of single-walled nanotubes.
How the structural properties of the fullerene
nanotubes change with conformation is one of the
most important questions to be answered about these In earlier work, we found this relationship was well
new materials. In particular, two properties are most observed, using empirical bond-order potentials for all
apt for study with the LDF approach: how does the nanotubes with radii less than 0.9 nm, and for a range
band gap change with nanotube diameter, and how of serpentine nanotubes using the LDF method. As
does the strain energy change with nanotube diameter? part of our studies, we have carried out first-principles
We have studied these questions extensively using em- LDF calculations on a representative sample of chi-
pirical methods[ 10-14,23], and are currently working ral nanotubes. Iijima and Ichihashi[7] have recently
on a comprehensive study of the band gaps, strain en- reported the synthesis of single-shell fullerene nano-
ergies, and other properties using the LDF approach. tubes with diameters of about 1 nm, using the gas-phase
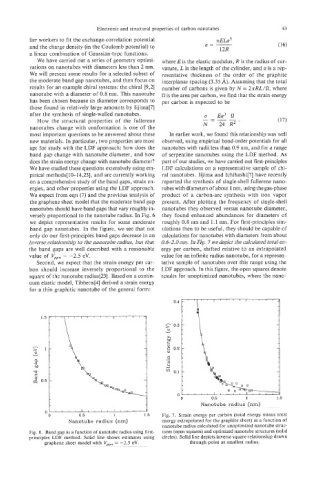
We expect from eqn (7) and the previous analysis of product of a carbon-arc synthesis with iron vapor
the graphene sheet model that the moderate band gap present. After plotting the frequency of single-shell
nanotubes should have band gaps that vary roughly in- nanotubes they observed versus nanotube diameter,
versely proportional to the nanotube radius. In Fig. 6 they found enhanced abundances for diameters of
we depict representative results for some moderate roughly 0.8 nm and 1.1 nm. For first-principles sim-
band gap nanotubes. In the figure, we see that not ulations then to be useful, they should be capable of
only do our first-principles band gaps decrease in an calculations for nanotubes with diameters from about
inverse relationship to the nanotube radius, but that 0.6-2.0 nm. In Fig. 7 we depict the calculated total en-
the band gaps are well described with a reasonable ergy per carbon, shifted relative to an extrapolated
value of V,, - -2.5 eV. value for an infinite radius nanotube, for a represen-
Second, we expect that the strain energy per car- tative sample of nanotubes over this range using the
bon should increase inversely proportional to the LDF approach. In this figure, the open squares denote
square of the nanotube radius[23]. Based on a contin- results for unoptimized nanotubes, where the nano-
uum elastic model, Tibbetts[4] derived a strain energy
for a thin graphitic nanotube of the general form:

0.4

0.3

c
2
.A
4
0.1

0
Nanotube radius (nm)
0
0 0.5 1 1.5 Fig. 7. Strain energy per carbon (total energy minus total
Nanotube radius (nm) energy extrapolated for the graphite sheet) as a function of
nanotube radius calculated for unoptimized nanotube struc-
Fig. 6. Band gap as a function of nanotube radius using first- tures (open squares) and optimized nanotube structures (solid
principles LDF method. Solid line shows estimates using circles). Solid line depicts inverse square relationship drawn
graphene sheet model with V,, = -2.5 eV. through point at smallest radius.