Page 98 - Carbon Nanotubes

88 A. FONSECA al.
et

-
I I
I -1
-1
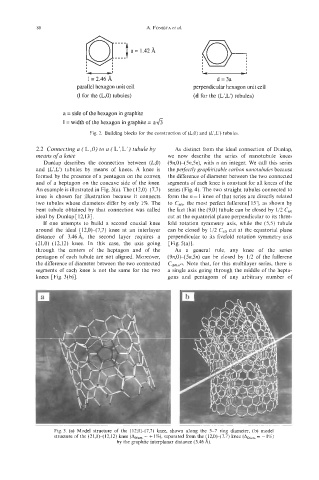
1 = 2.46 A d=3a
parallel hexagon unit cell perpendicular hexagon unit cell
(1 for the (L,O) tubules) (d for the (L',L') tubules)
a = side of the hexagon in graphite
1 = width of the hexagon in graphite = a6

Fig. 2. Building blocks for the construction of (L,O) and (L',L') tubules.

2.2 Connecting a (L ,0) to a (L',L') tubule by As distinct from the ideal connection of Dunlap,
means of a knee we now describe the series of nanotubule knees
Dunlap describes the connection between (L,O) (9n,0)-(5n,5n), with n an integer. We call this series
and (L',L') tubules by means of knees. A knee is the perfectly graphitizable carbon nanotubules because
formed by the presence of a pentagon on the convex the difference of diameter between the two connected
and of a heptagon on the concave side of the knee. segments of each knee is constant for all knees of the
An example is illustrated in Fig. 3(a). The (12,O)-( 7,7) series (Fig. 4). The two straight tubules connected to
knee is chosen for illustration because it connects form the n= 1 knee of that series are directly related
two tubules whose diameters differ by only 1%. The to C60, the most perfect fullerene[15], as shown by
bent tubule obtained by that connection was called the fact that the (9,O) tubule can be closed by 1/2 C60
ideal by Dunlap[ 12,131. cut at the equatorial plane perpendicular to its three-
If one attempts to build a second coaxial knee fold rotation symmetry axis, while the (53) tubule
around the ideal (12,O)-(7,7) knee at an interlayer can be closed by 1/2 C60 cut at the equatorial plane
distance of 3.46A, the second layer requires a perpendicular to its fivefold rotation symmetry axis
(21,O)-( 12,12) knee. In this case, the axis going [Fig. 5(a)].
through the centers of the heptagon and of the As a general rule, any knee of the series
pentagon of each tubule are not aligned. Moreover, (9n,0)-(5n,5n) can be closed by 1/2 of the fullerene
the difference of diameter between the two connected C(60,n~). Note that, for this multilayer series, there is
segments of each knee is not the same for the two a single axis going through the middle of the hepta-
knees [Fig. 3(b)]. gons and pentagons of any arbitrary number of

Fig. 3. (a) Model structure of the (12,O)-(7,7) knee, shown along the 5-7 ring diameter, (b) model
structure of the (21,O)-( 12,12) knee (ADiam, = + l%), separated from the (12,O)-(7,7) knee (ADiam. = - 1%)
by the graphite interplanar distance (3.46 A).