Page 101 - Carbon Nanotubes

Graphitizable coiled carbon nanotubes 91
Table 1. Characteristics of some knees with minimal diameter difference

0 3 2 - 15.5 2.53
0 4 2 13.4 2.92
0 5 3 - 3.9 3.99
0 6 3 13.4 4.38
0 7 4 1 .o 5.45
0 8 5 - 8.2 6.52
1 0 0 3.8 6.914
1 1 1 - 3.9 7.98
1 2 1 5.5 8.38
1 3 2 - 1.0 9.44
1 4 3 - 6.6 10.51
1 5 3 1 .o 10.91
1 6 4 - 3.9 11.98
1 7 4 2.6 12.37
1 8 5 - 1.9 13.44
2 0 0 3.8 13.83

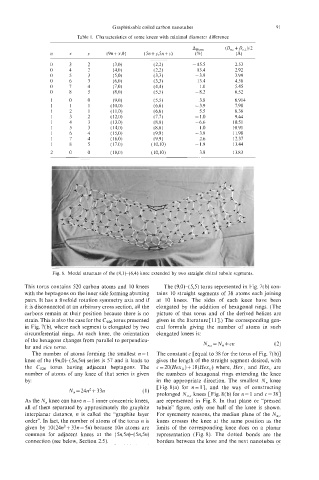
Fig. 6. Model structure of the (8,l)-(6,4) knee extended by two straight chiral tubule segments.

This torus contains 520 carbon atoms and 10 knees The (9,O)-( 5,s) torus represented in Fig. 7( b) con-
with the heptagons on the inner side forming abutting tains 10 straight segments of 38 atoms each joining
pairs. It has a fivefold rotation symmetry axis and if at 10 knees. The sides of each knee have been
it is disconnected at an arbitrary cross section, all the elongated by the addition of hexagonal rings. (The
carbons remain at their position because there is no picture of that torus and of the derived helices are
strain. This is also the case for the C9,,,, torus presented given in the literature[ 111.) The corresponding gen-
in Fig. 7(b), where each segment is elongated by two eral formula giving the number of atoms in such
circumferential rings. At each knee, the orientation elongated knees is:
of the hexagons changes from parallel to perpendicu-
lar and vice versa. N,,= = N, + cn (2)
The number of atoms forming the smallest n=l The constant c [equal to 38 for the torus of Fig. 7( b)]
knee of the (9n,0)-(5n,5n) series is 57 and it leads to gives the length of the straight segment desired, with
the C520 torus having adjacent heptagons. The c = 20(Hex,) + 18 (Hexii) where, Hex, and Hexi, are
number of atoms of any knee of that series is given the numbers of hexagonal rings extending the knee
by: in the appropriate direction. The smallest N, knee
[Fig. 8(a) for n=l], and the way of constructing
N, = 24n2 + 33n (1) prolonged N,,c knees [Fig. 8( b) for n = 1 and c = 381
As the N, knee can have n- 1 inner concentric knees, are represented in Fig. 8. In that plane or “pressed
all of them separated by approximately the graphite tubule” figure, only one half of the knee is shown.
interplanar distance, n is called the “graphite layer For symmetry reasons, the median plane of the N,,c
order”. In fact, the number of atoms of the torus n is knees crosses the knee at the same position as the
given by 10(24n2+33n-5n) because 10n atoms are limits of the corresponding knee does on a planar
common for adjacent knees at the (5n,5n)-( 5n,5n) representation (Fig. 8). The dotted bonds are the
connection (see below, Section 2.5). borders between the knee and the next nanotubes or