Page 72 - Civil Engineering Formulas

R 2 k(1 – k 2 )
3 2 PL 2 6EI kx″(1 – k 2 – x″ 2 )
R 2 = Pk x″L (x″ < (1 – k)) R 2 x″ L 1 – k 2 k 3 1 – k 2 3
(l – k)L PL 3 = 3EI PL 3 6EI L

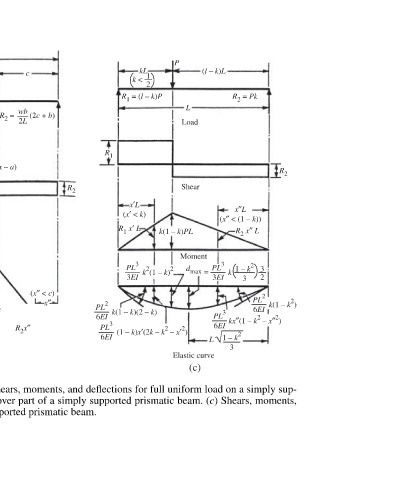
Load Shear Moment d max Elastic curve (c)
L
P k(1 – k)PL simply supported prismatic beam. (c) Shears, moments,
R 1 = (l – k)P
1 2 k 2 (1 – k) 2 (1 – k)x′(2k – k 2 – x′ 2 )
kL
k < x′L (x′ < k) R 1 x′ L PL 3 3EI k(1 – k)(2 – k)
R 1 PL 3 6EI
PL 2 6EI
R 2
(2c + b) (x″ < c) x″ Elastic-curve equations for prismatic beams: (a) Shears, moments, and deflections for full uniform load on a simply sup-

c
wb 2L R 2 x″
R 2 = R 1 – w (x – a) R 2c

L Load Shear 1 2w 1 R (a + Moment (b)
b R 2 1
(2c + b) R 1 w 2 (x – a) w R 1a – R x
w wb 2L x (a < x < a + b) a + R 1 x′
a
R = (x′ < a) x′ and deflections for a concentrated load at any point of a simply supported prismatic beam.
R 1 ported prismatic beam. (b) Shears and moments for uniform load over part of a

R
wL 2
R =
L 2 wL 2 8
– xwL 5wL 4 384EI Elastic curve
Load Shear Moment L c
L 1 2 (a)
w
wL 4 24EI
1 2
wL 2 xL 1 2
R = x < x(l – x)wL 2 x(l – 2x 2 + x 3 ) FIGURE 2.3
R 1 2 wL 3 24EI

32