Page 76 - Civil Engineering Formulas

(L + L′) 2 (L 2 – L′ 2 ) x′ 2 (4L′ 2 – L 3 + 3L′ 3 )
w x′L′ wL′x′ wL′ 2 2
L′ w 2L w 2L
R 2 = R 2 (L + L′) 2 (L – L′) 2 wL′ 24EI
wL′ wL′ 2 2

(L 2 – L′ 2 ) R 1 = wLx w 8L 2 L′ 2 L 2 Elastic curve (i)
L Load Shear Moment L 2 (1 – 2x 2 + x 2 ) –2L′ 2 (1 – x 2 )
w w 2L 1 – L′ 2 L 2 1 – L
R 1 = xL L 2

R 1 (L 2 – L′ 2 – xL 2 ) wL 2 x 24EI
wx 2

P P
PL 3 3EI
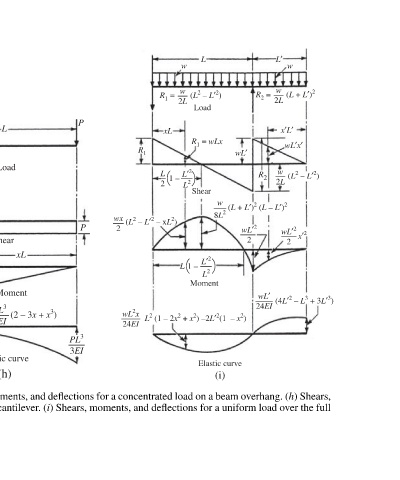
(2 – 3x + x 3 ) Elastic-curve equations for prismatic beams: (g) Shears, moments, and deflections for a concentrated load on a beam overhang. (h) Shears,

xL
Load Moment moments, and deflections for a concentrated load on the end of a prismatic cantilever. (i) Shears, moments, and deflections for a uniform load over the full
L Shear PL 3 3EI Elastic curve (h)
PxL
R = P

PL R PL

(L + L′)
PL′ 2 3EI
P
P 2(L + L′) – L′x′ (1 + x′)
x′L′
L′
Px′L′
PL′
P R 2 x(1 – x 2 ) length of a beam with overhang. (Continued)
L + L′ L Load Shear xPL′ PL′ 2 (1 – x′) 6EI Elastic curve (g)
R 2 = L PL′L 2 6EI
xL
P L Moment L 3 PL′L 2 3EI
R 1 = L′ 9 FIGURE 2.3

R 1 d max =

34