Page 81 - Civil Engineering Formulas

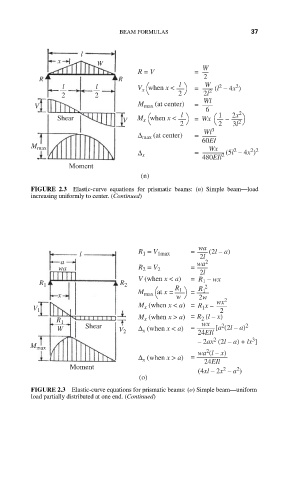
BEAM FORMULAS 37

l
x W
R = V = W
R R 2
l l V when x < l = W (l – 4x )
2
2
x
2 2 2 2l 2
V M max (at center) = Wl
6
l 1 2x 2
Shear V M when x < = Wx –
x
2 2 3l 2
Δ max (at center) = Wl 3
60EI
M max Wx
Δ x = 480EIl 2 (5l – 4x )
2 2
2
Moment
(n)
FIGURE 2.3 Elastic-curve equations for prismatic beams: (n) Simple beam—load
increasing uniformly to center. (Continued)

wa
= V = (2l – a)
l R 1 1max 2l
a wa 2
wa R = V 2 =
2
2l
V (when x < a) = R – wx
1
R 1 R 2 2
M at x = R 1 = R 1
x max w 2w 2
M (when x < a) = R 1 x – wx
x
V 1 2
(l – x)
R 1 M x (when x > a) = R 2 wx
2
W Shear V 2 Δ (when x < a) = 24EIl [a (2l – a) 2
x
2
3
– 2ax (2l – a)+ lx ]
M max
2
wa (l – x)
Δ x (when x > a) =
24EIl
Moment 2 2
(4xl – 2x – a )
(o)
FIGURE 2.3 Elastic-curve equations for prismatic beams: (o) Simple beam—uniform
load partially distributed at one end. (Continued)