Page 90 - Civil Engineering Formulas

BEAM FORMULAS 45

3 3
S
b n P n /W. These values are given in Fig. 2.8 for some common types
of loading.
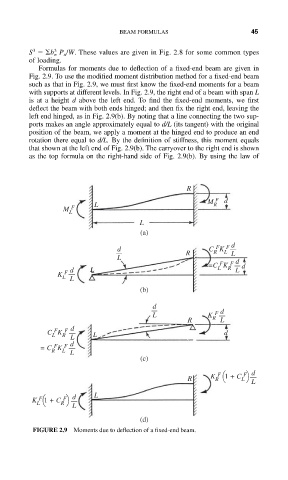
Formulas for moments due to deflection of a fixed-end beam are given in
Fig. 2.9. To use the modified moment distribution method for a fixed-end beam
such as that in Fig. 2.9, we must first know the fixed-end moments for a beam
with supports at different levels. In Fig. 2.9, the right end of a beam with span L
is at a height d above the left end. To find the fixed-end moments, we first
deflect the beam with both ends hinged; and then fix the right end, leaving the
left end hinged, as in Fig. 2.9(b). By noting that a line connecting the two sup-
ports makes an angle approximately equal to d/L (its tangent) with the original
position of the beam, we apply a moment at the hinged end to produce an end
rotation there equal to d/L. By the definition of stiffness, this moment equals
that shown at the left end of Fig. 2.9(b). The carryover to the right end is shown
as the top formula on the right-hand side of Fig. 2.9(b). By using the law of

R

M F d
L R
M F
L
L
(a)
F
d C K F d
R R L L
L
F
=C K F d d
d L L R L
F
K
L L
(b)
d
L K R F d
R L
F
C K F d d
L R L L
F
= C K F d
R L L
(c)
F
R K 1 + C L F d
R
L
F
K 1 + C F d L
L R L
(d)
FIGURE 2.9 Moments due to deflection of a fixed-end beam.