Page 132 - Classification Parameter Estimation & State Estimation An Engg Approach Using MATLAB

DISCRETE STATE VARIABLES 121

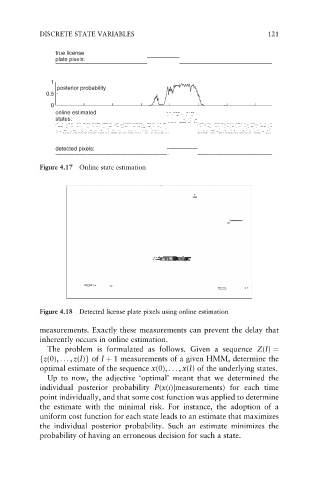
true license
plate pixels:

1
posterior probability
0.5
0
online estimated
states:

detected pixels:

Figure 4.17 Online state estimation

Figure 4.18 Detected license plate pixels using online estimation

measurements. Exactly these measurements can prevent the delay that
inherently occurs in online estimation.
The problem is formulated as follows. Given a sequence Z(I) ¼
fz(0), .. . , z(I)g of I þ 1 measurements of a given HMM, determine the
optimal estimate of the sequence x(0), ... , x(I) of the underlying states.
Up to now, the adjective ‘optimal’ meant that we determined the
individual posterior probability P(x(i)jmeasurements) for each time
point individually, and that some cost function was applied to determine
the estimate with the minimal risk. For instance, the adoption of a
uniform cost function for each state leads to an estimate that maximizes
the individual posterior probability. Such an estimate minimizes the
probability of having an erroneous decision for such a state.