Page 166 - Classification Parameter Estimation & State Estimation An Engg Approach Using MATLAB

NONPARAMETRIC LEARNING 155

(a) (b)
1

measure of eccentricity 0.6
0.8

0.4

1 0.2
0.8 1
0.6 0.8 0
0.4 0.4 0.6 0 0.2 0.4 0.6 0.8
0.2 0.2
0 0 measure of six-fold rotational symmetry

(c) (d)
1

measure of eccentricity 0.6
0.8

0.4

0.2
1
0.8
0.6 0.8 1
0.4 0.6 0
0.2 0.4 0 0.2 0.4 0.6 0.8
0 0 0.2 measure of six-fold rotational symmetry
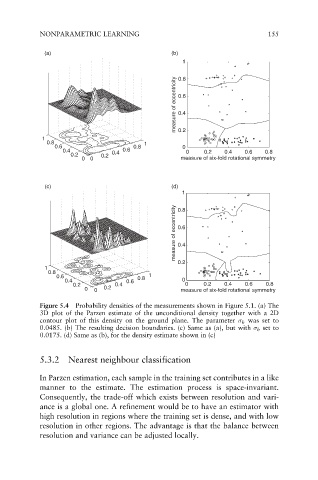
Figure 5.4 Probability densities of the measurements shown in Figure 5.1. (a) The
3D plot of the Parzen estimate of the unconditional density together with a 2D
contour plot of this density on the ground plane. The parameter h was set to
0.0485. (b) The resulting decision boundaries. (c) Same as (a), but with h set to
0.0175. (d) Same as (b), for the density estimate shown in (c)

5.3.2 Nearest neighbour classification

In Parzen estimation, each sample in the training set contributes in a like
manner to the estimate. The estimation process is space-invariant.
Consequently, the trade-off which exists between resolution and vari-
ance is a global one. A refinement would be to have an estimator with
high resolution in regions where the training set is dense, and with low
resolution in other regions. The advantage is that the balance between
resolution and variance can be adjusted locally.