Page 263 - Compact Numerical Methods For Computers

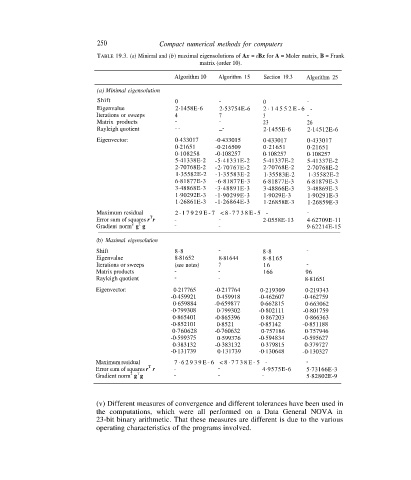
250 Compact numerical methods for computers

TABLE 19.3. (a) Minimal and (b) maximal eigensolutions of Ax = eBx for A = Moler matrix, B = Frank
matrix (order 10).

Algorithm 10 Algorithm 15 Section 19.3 Algorithm 25
(a) Minimal eigensolution
Shift 0 - 0 -
Eigenvalue 2·1458E-6 2·53754E-6 2 · 1 4 5 5 2 E - 6 -
Iterations or sweeps 4 7 3 -
Matrix products - - 23 26
Rayleigh quotient - - _- 2·1455E-6 2·14512E-6
Eigenvector: 0·433017 -0·433015 0·433017 0·433017
0·21651 -0·216509 0·21651 0·21651
0·108258 -0·108257 0·108257 0·108257
5·41338E-2 -5·41331E-2 5·41337E-2 5·41337E-2
2·70768E-2 -2·70767E-2 2·70768E-2 2·70768E-2
1·35582E-2 -1·35583E-2 1·35583E-2 1·35582E-2
6·81877E-3 -6·81877E-3 6·81877E-3 6·81879E-3
3·48868E-3 -3·48891E-3 3·48866E-3 3·48869E-3
1·90292E-3 -1·90299E-3 1·9029E-3 1·90291E-3
1·26861E-3 -1·26864E-3 1·26858E-3 1·26859E-3
Maximum residual 2 · 1 7 9 2 9 E - 7 < 8 · 7 7 3 8 E - 5 - -
T
Error sum of squares r r - - 2·0558E-13 4·62709E-11
T
Gradient norm 2 g g - - 9·62214E-15
(b) Maximal eigensolution
Shift 8·8 - 8·8 -
Eigenvalue 8·81652 8·81644 8·8165
Iterations or sweeps (see notes) 7 16 -
Matrix products - - 166 96
Rayleigh quotient - - 8·81651
Eigenvector: 0·217765 -0·217764 0·219309 0·219343
-0·459921 0·459918 -0·462607 -0·462759
0·659884 -0·659877 0·662815 0·663062
-0·799308 0·799302 -0·802111 -0·801759
0·865401 -0·865396 0·867203 0·866363
-0·852101 0·8521 -0·85142 -0·851188
0·760628 -0·760632 0·757186 0·757946
-0·599375 0·599376 -0·594834 -0·595627
0·383132 -0·383132 0·379815 0·379727
-0·131739 0·131739 -0·130648 -0·130327
Maximum residual 7 · 6 2 9 3 9 E - 6 < 8 · 7 7 3 8 E - 5 - -
T
Error sum of squares r r - - 4·9575E-6 5·73166E-3
2
T
Gradient norm g g - - - 5·82802E-9
(v) Different measures of convergence and different tolerances have been used in
the computations, which were all performed on a Data General NOVA in
23-bit binary arithmetic. That these measures are different is due to the various
operating characteristics of the programs involved.