Page 246 - Computational Fluid Dynamics for Engineers

7.5 Applications of BLP 235

1000.0 r

eoo.o y

Mtehol's Formica
600.0 h
R»

400.0

200.0 h

0.0
0.5 1.0 2.0
R xlO" 6
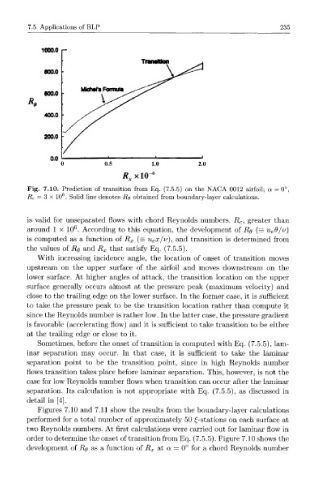
Fig. 7.10. Prediction of transition from Eq. (7.5.5) on the NACA 0012 airfoil; a = 0°,
6
= 3 x 10 . Solid line denotes i?# obtained from boundary-layer calculations.
R c
is valid for unseparated flows with chord Reynolds numbers. i? c , greater than
6
around 1 x 10 . According to this equation, the development of RQ (= u e6/v)
is computed as a function of R x (= u exjv), and transition is determined from
the values of RQ and R x that satisfy Eq. (7.5.5).
With increasing incidence angle, the location of onset of transition moves
upstream on the upper surface of the airfoil and moves downstream on the
lower surface. At higher angles of attack, the transition location on the upper
surface generally occurs almost at the pressure peak (maximum velocity) and
close to the trailing edge on the lower surface. In the former case, it is sufficient
to take the pressure peak to be the transition location rather than compute it
since the Reynolds number is rather low. In the latter case, the pressure gradient
is favorable (accelerating flow) and it is sufficient to take transition to be either
at the trailing edge or close to it.
Sometimes, before the onset of transition is computed with Eq. (7.5.5), lam-
inar separation may occur. In that case, it is sufficient to take the laminar
separation point to be the transition point, since in high Reynolds number
flows transition takes place before laminar separation. This, however, is not the
case for low Reynolds number flows when transition can occur after the laminar
separation. Its calculation is not appropriate with Eq. (7.5.5), as discussed in
detail in [4].
Figures 7.10 and 7.11 show the results from the boundary-layer calculations
performed for a total number of approximately 50 ^-stations on each surface at
two Reynolds numbers. At first calculations were carried out for laminar flow in
order to determine the onset of transition from Eq. (7.5.5). Figure 7.10 shows the
development of RQ as a function of R x at a = 0° for a chord Reynolds number