Page 291 - Computational Modeling in Biomedical Engineering and Medical Physics

280 Computational Modeling in Biomedical Engineering and Medical Physics

and the dissipated magnetic power density (using the effective value of H 0 )
2
_ q 5 f ΔUj 5 μ ωχvH : ð8:21Þ
mg cycle 0 0
This specific heat source contributes to the local heating that adds to the Joule or
SAR heating produced by the electric field. For the combined, electric and magnetic
heating, the bioheat Eq. (8.11a) then becomes

@T 2 2 2
ρC 5 kr T 2 ρ C b ω b T 2 T b Þ 1 Q met 1 σ tissue E 1 μ ωχvH : ð8:22Þ
ð
b
0
@t |fflfflffl{zfflfflffl} |fflfflfflfflfflffl{zfflfflfflfflfflffl}
Q electric Q magnetic
For a collection of MNPs, of concentration n and radius r, the magnetic heat
4 3 2
source terms become nπr μ ωχvH . When MNPs are injected in the tumor both
3 0
magnetic and electric fields produce heat that is a superposition of two quadratic
forms, the squares of the electric and magnetic fields' strengths.

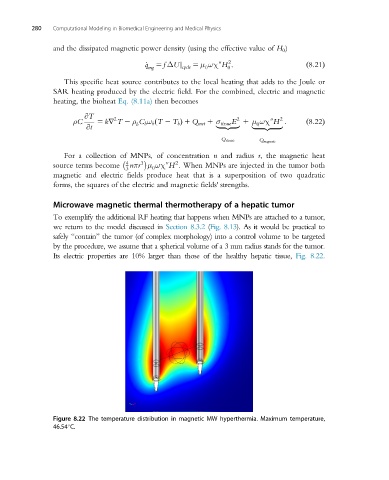
Microwave magnetic thermal thermotherapy of a hepatic tumor
To exemplify the additional RF heating that happens when MNPs are attached to a tumor,
we return to the model discussed in Section 8.3.2 (Fig. 8.13). As it would be practical to
safely “contain” the tumor (of complex morphology) into a control volume to be targeted
by the procedure, we assume that a spherical volume of a 3 mm radius stands for the tumor.
Its electric properties are 10% larger than those of the healthy hepatic tissue, Fig. 8.22.

Figure 8.22 The temperature distribution in magnetic MW hyperthermia. Maximum temperature,
46.54 C.