Page 697 - Discrete Mathematics and Its Applications

676 10 / Graphs

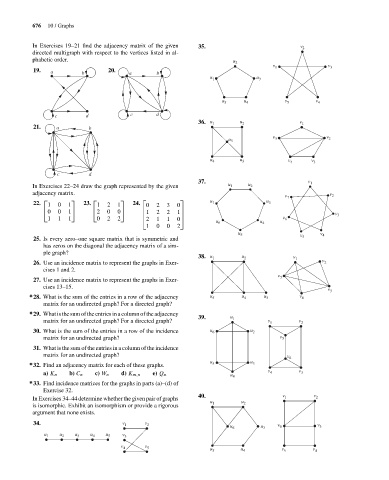
In Exercises 19–21 find the adjacency matrix of the given 35. v 2
directed multigraph with respect to the vertices listed in al-
phabetic order. u 2
v 1 v 3
19. a b 20. a b
u 1 u 3

u 5 u 4 v 5 v 4

c d c d
36. u 1 u 2 v 1
21. a b
v v
u 5 5 2

u 4 u 3 v 4 v 3

c d
37. v 1
In Exercises 22–24 draw the graph represented by the given u 1 u 2
adjacency matrix. v 2
v 7
⎡ ⎤ ⎡ ⎤ ⎡ ⎤
22. 1 0 1 23. 1 2 1 24. 0 2 3 0 u 7 u 3
⎣ 0 0 1 ⎦ ⎣ 2 0 0 ⎦ ⎢ 1 2 2 1 ⎥ v 3
⎢
⎥
1 1 1 0 2 2 ⎣ 2 1 1 0 ⎦ v 6
u 6 u 4
1 0 0 2
u 5 v v 4
25. Is every zero–one square matrix that is symmetric and 5
has zeros on the diagonal the adjacency matrix of a sim-
ple graph?
38. u 1 u 2 v 1
26. Use an incidence matrix to represent the graphs in Exer- v 2
cises 1 and 2.
v 5
27. Use an incidence matrix to represent the graphs in Exer-
cises 13–15.
v 3
∗ 28. What is the sum of the entries in a row of the adjacency u 5 u 4 u 3 v 4
matrix for an undirected graph? For a directed graph?
∗ 29. What is the sum of the entries in a column of the adjacency u
matrix for an undirected graph? For a directed graph? 39. 1 v 1 v 2
30. What is the sum of the entries in a row of the incidence u 6 u 2
matrix for an undirected graph? v 5
31. What is the sum of the entries in a column of the incidence
matrix for an undirected graph? v 6
u u
∗ 32. Find an adjacency matrix for each of these graphs. 5 3
v 4 v 3
a) K n b) C n c) W n d) K m,n e) Q n u 4
∗ 33. Find incidence matrices for the graphs in parts (a)–(d) of
Exercise 32.
40. v 1 v 2
In Exercises 34–44 determine whether the given pair of graphs
u 1 u 2
is isomorphic. Exhibit an isomorphism or provide a rigorous
argument that none exists.
34. v 1 v 2 v v
u 6 u 3 6 3
u 1 u 2 u 3 u 4 u 5 v 3

v 4 v 5 u 5 u 4 v 5 v 4