Page 702 - Discrete Mathematics and Its Applications

10.4 Connectivity 681

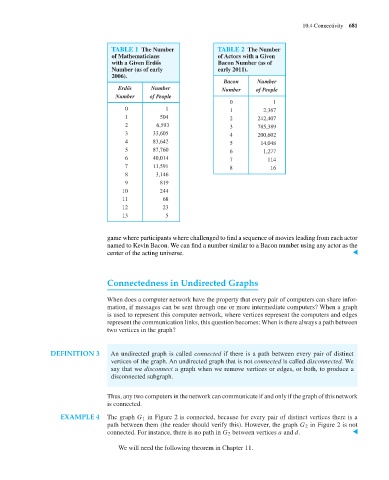
TABLE 1 The Number TABLE 2 The Number
of Mathematicians of Actors with a Given
with a Given Erd˝os Bacon Number (as of
Number (as of early early 2011).
2006).
Bacon Number
Erd˝os Number Number of People
Number of People
0 1
0 1 1 2,367
1 504 2 242,407
2 6,593 3 785,389
3 33,605 4 200,602
4 83,642 5 14,048
5 87,760 6 1,277
6 40,014 7 114
7 11,591 8 16
8 3,146
9 819
10 244
11 68
12 23
13 5

game where participants where challenged to find a sequence of movies leading from each actor
named to Kevin Bacon. We can find a number similar to a Bacon number using any actor as the
center of the acting universe. ▲

Connectedness in Undirected Graphs

When does a computer network have the property that every pair of computers can share infor-
mation, if messages can be sent through one or more intermediate computers? When a graph
is used to represent this computer network, where vertices represent the computers and edges
represent the communication links, this question becomes: When is there always a path between
two vertices in the graph?

DEFINITION 3 An undirected graph is called connected if there is a path between every pair of distinct
vertices of the graph. An undirected graph that is not connected is called disconnected.We
say that we disconnect a graph when we remove vertices or edges, or both, to produce a
disconnected subgraph.

Thus, any two computers in the network can communicate if and only if the graph of this network
is connected.

EXAMPLE 4 The graph G 1 in Figure 2 is connected, because for every pair of distinct vertices there is a
path between them (the reader should verify this). However, the graph G 2 in Figure 2 is not
connected. For instance, there is no path in G 2 between vertices a and d. ▲

We will need the following theorem in Chapter 11.