Page 297 - Design for Six Sigma a Roadmap for Product Development

Axiomatic Design 267

of a pair of mating gears are tangential to each other. However, the pitch
diameters are hypothetical circles that can’t be measured directly. The func-
tion of the gear is to “transfer speed.” This function can be mapped to many
design parameters that can be grouped basically into two subsets of DPs: a
geometric subset and a material property (stiffness, hardness, etc.) subset.
The diameter of the pitch circle PD follows a normal distribution as a result
2
2
of manufacturing process variability: PD f(PD) (1/ 2 ) e PD /2 2 .
Then, we have
h(f) f(PD) ln f(PD)
PD 2
f(PD) ln 2 2
2 2
1 2
2 E (PD ) ln 2 2
2
2
ln 2 e nats (8.14)
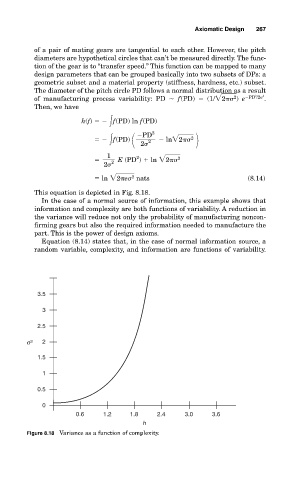
This equation is depicted in Fig. 8.18.
In the case of a normal source of information, this example shows that
information and complexity are both functions of variability. A reduction in
the variance will reduce not only the probability of manufacturing noncon-
firming gears but also the required information needed to manufacture the
part. This is the power of design axioms.
Equation (8.14) states that, in the case of normal information source, a
random variable, complexity, and information are functions of variability.

3.5

3
2.5

σ 2 2

1.5
1

0.5

0
0.6 1.2 1.8 2.4 3.0 3.6
h
Figure 8.18 Variance as a function of complexity.