Page 235 - Design of Reinforced Masonry Structures

4.98 CHAPTER FOUR

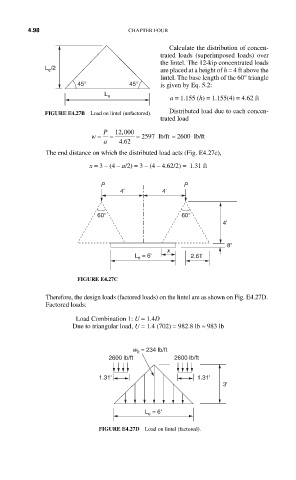
Calculate the distribution of concen-
trated loads (superimposed loads) over
the lintel. The 12-kip concentrated loads
L /2 are placed at a height of h = 4 ft above the
e
lintel. The base length of the 60° triangle
45° 45° is given by Eq. 5.2:
L e
a = 1.155 (h) = 1.155(4) = 4.62 ft
FIGURE E4.27B Load on lintel (unfactored). Distributed load due to each concen-
trated load
,
w = P = 12 000 = 2597 lb/ft ≈ 2600 lb/ft
a 462
.
The end distance on which the distributed load acts (Fig. E4.27c),
x = 3 – (4 – a/2) = 3 – (4 – 4.62/2) = 1.31 ft

P P
4' 4'

60° 60°
4'

8"
x
L = 6' 2.61'
e

FIGURE E4.27C

Therefore, the design loads (factored loads) on the lintel are as shown on Fig. E4.27D.
Factored loads:

Load Combination 1: U = 1.4D
Due to triangular load, U = 1.4 (702) = 982.8 lb ≈ 983 lb

w 0 = 234 lb/ft
2600 lb/ft 2600 lb/ft

1.31' 1.31'
3'

L e = 6'

FIGURE E4.27D Load on lintel (factored).