Page 77 - Designing Autonomous Mobile Robots : Inside the Mindo f an Intellegent Machine

Chapter 5

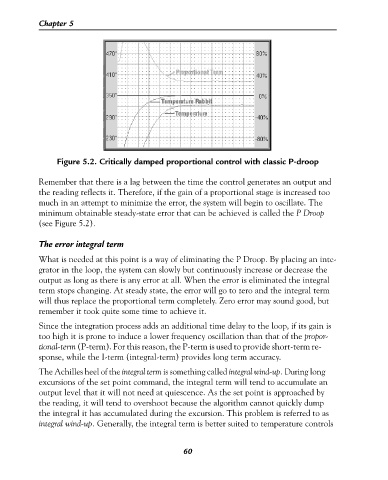
Figure 5.2. Critically damped proportional control with classic P-droop

Remember that there is a lag between the time the control generates an output and
the reading reflects it. Therefore, if the gain of a proportional stage is increased too
much in an attempt to minimize the error, the system will begin to oscillate. The
minimum obtainable steady-state error that can be achieved is called the P Droop
(see Figure 5.2).

The error integral term
What is needed at this point is a way of eliminating the P Droop. By placing an inte-
grator in the loop, the system can slowly but continuously increase or decrease the
output as long as there is any error at all. When the error is eliminated the integral
term stops changing. At steady state, the error will go to zero and the integral term
will thus replace the proportional term completely. Zero error may sound good, but
remember it took quite some time to achieve it.

Since the integration process adds an additional time delay to the loop, if its gain is
too high it is prone to induce a lower frequency oscillation than that of the propor-
tional-term (P-term). For this reason, the P-term is used to provide short-term re-
sponse, while the I-term (integral-term) provides long term accuracy.

The Achilles heel of the integral term is something called integral wind-up. During long
excursions of the set point command, the integral term will tend to accumulate an
output level that it will not need at quiescence. As the set point is approached by
the reading, it will tend to overshoot because the algorithm cannot quickly dump
the integral it has accumulated during the excursion. This problem is referred to as
integral wind-up. Generally, the integral term is better suited to temperature controls

60