Page 92 - Designing Autonomous Mobile Robots : Inside the Mindo f an Intellegent Machine

Closed Loop Controls, Rabbits and Hounds

Rabbits chasing rabbits

The smoother the rabbit’s motion, the more likely the servo will be able to track it
closely. For this reason, linear approximations (trapezoidal profiles) are not generally
acceptable. Such a profile demands infinite acceleration at the knee points. Com-
mand curves with low second derivatives (jerk term) are also essential in some cases.

When we ascend to the level of making a robot navigate, there is much more in-
volved than a simple single-axis servo chasing its rabbit. We must first generate a
position rabbit that runs through imaginary space, and then determine the behavior
we want from the steering and/or drive motors in order to follow it. If we are execut-
ing an arc, then the steering rabbit must be slaved to the drive rabbit, and both must
be slaved to the position rabbit.
We will discuss some of these issues in the following chapters. The important thing
to remember is that the most elaborate building is made of lots of simple blocks.
Likewise, all complex systems are constructed from simpler blocks. If these blocks
are understood and perfected, they can be used to create systems that dependably
generate very complex behavior.

Conclusions

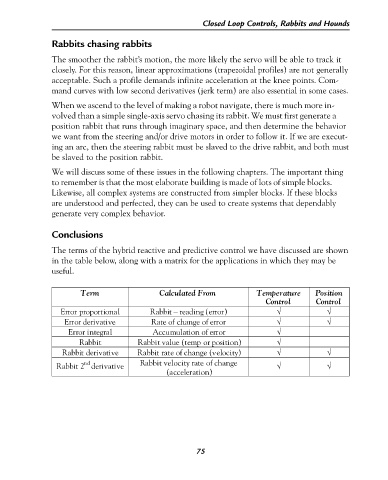
The terms of the hybrid reactive and predictive control we have discussed are shown
in the table below, along with a matrix for the applications in which they may be
useful.

Term Calculated From Temperature Position
Control Control
Error proportional Rabbit – reading (error) √ √
Error derivative Rate of change of error √ √
Error integral Accumulation of error √
Rabbit Rabbit value (temp or position) √
Rabbit derivative Rabbit rate of change (velocity) √ √
nd
Rabbit 2 derivative Rabbit velocity rate of change √ √
(acceleration)

75