Page 192 - Determinants and Their Applications in Mathematical Physics

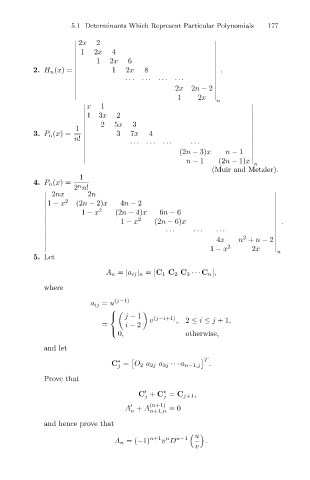
5.1 Determinants Which Represent Particular Polynomials 177
2x 2

1 2x 4

1 2x 6

1 2x 8 .

2. H n (x)=

··· ··· ··· ···

2x

2n − 2
1 2x

n
x 1

1 3x 2

2 5x 3

3. P n (x)= 1 3 7x 4
n!
··· ··· ··· ···

(2n − 3)x n − 1

n − 1 (2n − 1)x

n
(Muir and Metzler).
1
4. P n (x)=
2 n!
n
2nx 2n

1 − x 2 (2n − 2)x 4n − 2

1 − x (2n − 4)x 6n − 6
2

1 − x (2n − 6)x .
2

··· ··· ···

4x
2
n + n − 2
1 − x 2x
2
n
5. Let

A n = |a ij | n = C 1 C 2 C 3 ··· C n ,

where
a ij = u (j−1)


j − 1
 v (j−i+1) , 2 ≤ i ≤ j +1,
= i − 2
0, otherwise,

and let

∗ T
.
C = O 2 a 2j a 3j ··· a n−1,j
j
Prove that

∗
C + C = C j+1 ,
j j
(n+1)
A + A =0

n
n+1,n
and hence prove that
u
1 2
n−1
v D
A n =(−1) n+1 n .
v