Page 73 - Determinants and Their Applications in Mathematical Physics
P. 73
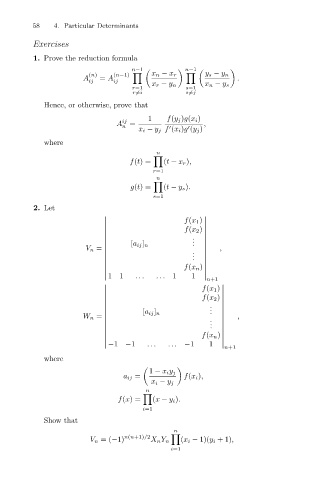
58 4. Particular Determinants
Exercises
1. Prove the reduction formula
n−1
n−1
(n) (n−1)
A = A x n − x r y s − y n .
ij ij
r=1 x r − y n s=1 x n − y s
r =i s=j
Hence, or otherwise, prove that
1 f(y j )g(x i )
A = ,
ij
x i − y j f (x i )g (y j )
n
where
n
f(t)= (t − x r ),
r=1
n
g(t)= (t − y s ).
s=1
2. Let
f(x 1 )
f(x 2 )
.
.
.
V n = [a ij ] n ,
.
.
.
f(x n )
11 ... ... 1 1
n+1
f(x 1 )
f(x 2 )
.
.
.
W n = [a ij ] n ,
.
.
.
f(x n )
−1 −1 ... ... −1 1
n+1
where
a ij = 1 − x i y j f(x i ),
n x i − y j
f(x)= (x − y i ).
i=1
Show that
n
n(n+1)/2
V n =(−1) X n Y n (x i − 1)(y i +1),
i=1