Page 297 - Dust Explosions in the Process Industries

266 Dust Explosions in the Process Industries

The linear rate at which a laminar combustion wave or reaction zone propagates rel-
ative to the unburned gas of a flammable mixture is called thefundamental or laminar
burning velocity, commonly denoted S,. As pointed out by Kuchta (1985), this velocity
is a fundamentalproperty of the mixture and depends primarily on the thermal diffusivity
A/pC, of the unburned gas, where A is the thermal conductivity, p is the density, and C,
is the specific heat at constant pressure of the unburned gas, and on the chemical reac-
tion rate and heat of combustion of the gas. The reaction zone in a premixed gas is nor-
mally quite thin, on the order of 1 111111.According to the classical Mallard-le Chatelier
(1883) theory, the fundamental laminar burning velocity of a homogeneous gas mixture
equals

(4.16)

where Tiis the ignition temperature of the gas mixture and L is the thickness of the reac-
tion zone. One problem with this theory is that a relevant value of Tiis normally not known
for a given gas mixture. The fundamental limitation of the theory is that it does not relate
S, to the heat release rate. Therefore, more refined theories have been developed, as are
mentioned here.
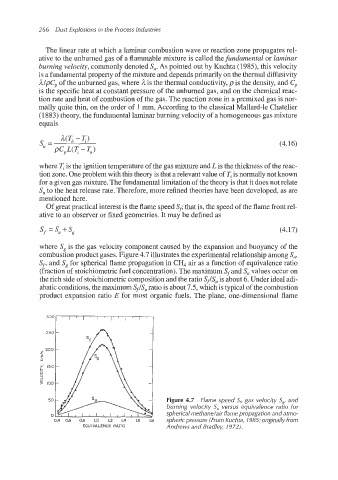
Of great practical interest is the flame speedS’ that is, the speed of the flame front rel-
ative to an observer or fixed geometries. It may be defined as

Sf = S, +S, (4.17)

where S, is the gas velocity component caused by the expansion and buoyancy of the
combustion product gases. Figure 4.7 illustratesthe experimentalrelationship among S,,
S’, and S, for spherical flame propagation in CH, air as a function of equivalenceratio
(fraction of stoichiometricfuel concentration).The maximum Sf and S, values occur on
the rich side of stoichiometriccomposition and the ratio S’/S, is about 6. Under ideal adi-
abatic conditions,the maximum S,/S, ratio is about 7.5, which is typical of the combustion
product expansion ratio E for most organic fuels. The plane, one-dimensional flame

Figure 4.7 Flame speed Sfi gas velocity Sg: and
burning velocity S, versus equivalence ratio for
sphericalmethane/air flame propagation and atmo-
sphericpressure (From Kuchta, 1985;originallyfrom
EQUIVALENCE RATIO Andrews and Bradley, 1972).