Page 497 - Dust Explosions in the Process Industries

464 Dust Explosions in the Process Industries

referring to more recent work by several workers. In particular, attempts at correlating
empirical turbulence factors with the Reynolds number of the flow of the burning cloud
were evaluated.

6.5.8
THEORY BY SWIFT

Swift (1988) proposed a venting equation implying that the maximum pressure in the
vented vessel is proportional to the square of the burning velocity of the dust cloud. A
turbulence factor, obtained from correlation with experimental data, was incorporated
in the burning velocity, as in the case of Nagy and Verakis.

6.5.9
THEORY BY URAL

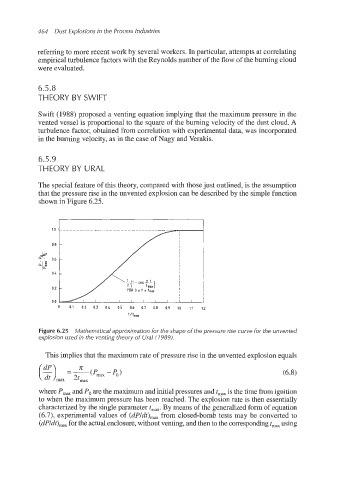
The special feature of this theory, compared with those just outlined, is the assumption
that the pressure rise in the unvented explosion can be describedby the simple function
shown in Figure 6.25.

10

0.8

$ 0.6
CL
0.4

0.2
0.0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2
t’tmax

Figure 6.25 Mathematical approximation for the shape of the pressure rise curve for the unvented
explosion used in the venting theory of Ural(l989).

This implies that the maximum rate of pressure rise in the unvented explosion equals

where P,, and Po are the maximum and initial pressures and tm, is the time from ignition
to when the maximum pressure has been reached. The explosion rate is then essentially
characterized by the single parameter tma,.By means of the generalized form of equation
(6.7), experimental values of (dPldt),, from closed-bomb tests may be converted to
(dPldt),, for the actualenclosure,without venting, and then to the correspondingtm, using