Page 55 - Dynamic Loading and Design of Structures
P. 55
Page 38
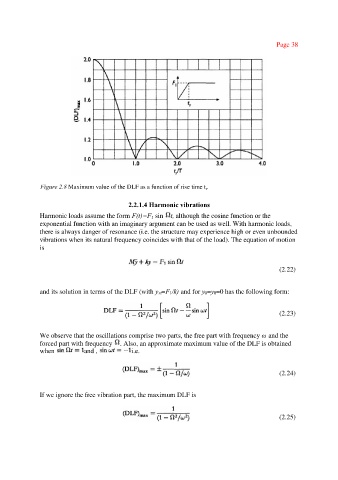
Figure 2.8 Maximum value of the DLF as a function of rise time t .
r
2.2.1.4 Harmonic vibrations
Harmonic loads assume the form F(t)=F sin t, although the cosine function or the
1
exponential function with an imaginary argument can be used as well. With harmonic loads,
there is always danger of resonance (i.e. the structure may experience high or even unbounded
vibrations when its natural frequency coincides with that of the load). The equation of motion
is
(2.22)
and its solution in terms of the DLF (with y st=F1/k) and for y0=y0=0 has the following form:
(2.23)
We observe that the oscillations comprise two parts, the free part with frequency ωand the
forced part with frequency . Also, an approximate maximum value of the DLF is obtained
when and , i.e.
(2.24)
If we ignore the free vibration part, the maximum DLF is
(2.25)