Page 92 - Dynamics and Control of Nuclear Reactors

7.9 Destabilizing negative feedback: A physical explanation 85

0.8
K=5
Step response (variable x in the model) –0.2 0
0.6
K=10
K=15
0.4
0.2

–0.4
–0.6
–0.8
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
Time (s)
FIG. 7.9
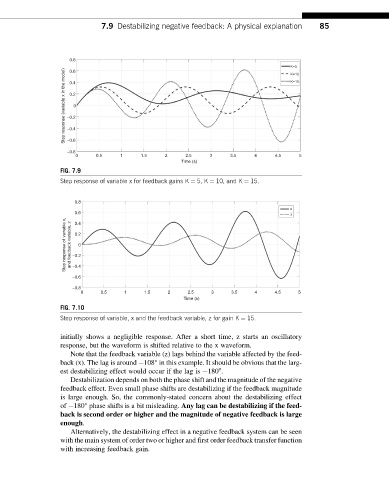
Step response of variable x for feedback gains K ¼ 5, K ¼ 10, and K ¼ 15.

0.8
x
0.6 z
Step response of variable x, and feedback variable, z –0.2 0
0.4
0.2

–0.4
–0.6
–0.8
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
Time (s)
FIG. 7.10
Step response of variable, x and the feedback variable, z for gain K ¼ 15.

initially shows a negligible response. After a short time, z starts an oscillatory
response, but the waveform is shifted relative to the x waveform.
Note that the feedback variable (z) lags behind the variable affected by the feed-
back (x). The lag is around 108° in this example. It should be obvious that the larg-
o
est destabilizing effect would occur if the lag is 180 .
Destabilization depends on both the phase shift and the magnitude of the negative
feedback effect. Even small phase shifts are destabilizing if the feedback magnitude
is large enough. So, the commonly-stated concern about the destabilizing effect
of 180° phase shifts is a bit misleading. Any lag can be destabilizing if the feed-
back is second order or higher and the magnitude of negative feedback is large
enough.
Alternatively, the destabilizing effect in a negative feedback system can be seen
with the main system of order two or higher and first order feedback transfer function
with increasing feedback gain.