Page 275 - Electrical Properties of Materials

Exercises 257

τ = τ 0 exp(H/kT) of one of the plates, one-third of its area is separated from
the dielectric by an air-filled gap of thickness 1 μm. The re-
(where τ 0 and H are constants) both of the experimental
curves can be approximated. Find τ 0 and H. maining two-thirds of the plate and the whole of the second
plate are in intimate contact with the dielectric. The break-
If a steady electric field is applied to thoria at 500 K, then –1 –1
down field E b is 2.0 MV m for the dielectric and 3.0 MV m
suddenly removed, indicate how the electric flux density will
for air, r is 1000. Discuss the effect of the gap (compared
change with time.
with a gap-free capacitor), on (a) the capacitance and (b) the
10.6. A more general time-varying relationship between the breakdown voltage.
electric displacement D and the electric field E may be
assumed to have the form 10.9. Derive an expression for the gain of the piezoelectric
dD dE ultrasonic amplifier (Hutson, McFee, and White (1961), Phys.
D + a = bE + c Rev. Lett., 7, 237).
dt dt
where a, b, c are constants. Determine the values of these [Hint: In the one-dimensional case we can work in terms of
constants in terms of s , the static dielectric constant, ∞ ,the scalar quantities. Our variables are: , D, T, S, J, N e .The
high-frequency dielectric constant, and τ, the relaxation time equations available are: eqns (10.58) and (10.59) for the rela-
for dipoles under constant electric field conditions. tionship between the mechanical and electrical quantities, the
equation for the electron current including both a conduction
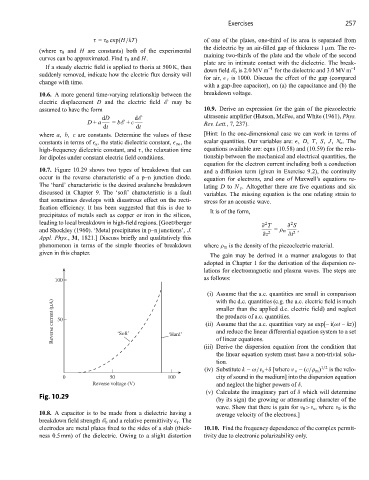
10.7. Figure 10.29 shows two types of breakdown that can and a diffusion term (given in Exercise 9.2), the continuity
occur in the reverse characteristic of a p–n junction diode. equation for electrons, and one of Maxwell’s equations re-
The ‘hard’ characteristic is the desired avalanche breakdown lating D to N e . Altogether there are five equations and six
discussed in Chapter 9. The ‘soft’ characteristic is a fault variables. The missing equation is the one relating strain to
that sometimes develops with disastrous effect on the recti- stress for an acoustic wave.
fication efficiency. It has been suggested that this is due to
It is of the form,
precipitates of metals such as copper or iron in the silicon,
leading to local breakdown in high-field regions. [Goetzberger 2 2
∂ T ∂ S
and Shockley (1960). ‘Metal precipitates in p–n junctions’, J. ∂z 2 = ρ m ∂t 2 ,
Appl. Phys., 31, 1821.] Discuss briefly and qualitatively this
phenomenon in terms of the simple theories of breakdown where ρ m is the density of the piezoelectric material.
given in this chapter. The gain may be derived in a manner analogous to that
adopted in Chapter 1 for the derivation of the dispersion re-
lations for electromagnetic and plasma waves. The steps are
100 as follows:

(i) Assume that the a.c. quantities are small in comparison
with the d.c. quantities (e.g. the a.c. electric field is much
Reverse current (μA) 50 ‘Soft’ ‘Hard’ (ii) Assume that the a.c. quantities vary as exp[– i(ωt – kz)]
smaller than the applied d.c. electric field) and neglect
the products of a.c. quantities.

and reduce the linear differential equation system to a set
of linear equations.
(iii) Derive the dispersion equation from the condition that
the linear equation system must have a non-trivial solu-
tion.
(iv) Substitute k = ω/ν s +δ [where ν s =(c/ρ m ) 1/2 is the velo-
0 50 100 city of sound in the medium] into the dispersion equation
Reverse voltage (V) and neglect the higher powers of δ.
(v) Calculate the imaginary part of δ which will determine
Fig. 10.29
(by its sign) the growing or attenuating character of the
wave. Show that there is gain for ν 0 >ν s ,where ν 0 is the
10.8. A capacitor is to be made from a dielectric having a average velocity of the electrons.]
breakdown field strength E b and a relative permittivity r .The
electrodes are metal plates fixed to the sides of a slab (thick- 10.10. Find the frequency dependence of the complex permit-
ness 0.5 mm) of the dielectric. Owing to a slight distortion tivity due to electronic polarizability only.