Page 313 - Electromagnetics

RHCP
4 LHCP

3
ω/ω 0 RHCP

2 Light Line stopband

1
RHCP
0
0 1 2 3 4 5
β/( /v )
c
0
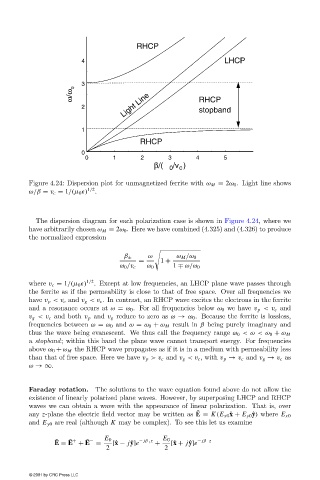
Figure 4.24: Dispersion plot for unmagnetized ferrite with ω M = 2ω 0 . Light line shows
ω/β = v c = 1/(µ 0 ) 1/2 .

The dispersion diagram for each polarization case is shown in Figure 4.24, where we
have arbitrarilychosen ω M = 2ω 0 . Here we have combined (4.325) and (4.326) to produce
the normalized expression

ω
β ± ω M /ω 0
= 1 +
ω 0 /v c ω 0 1 ∓ ω/ω 0
where v c = 1/(µ 0 ) 1/2 . Except at low frequencies, an LHCP plane wave passes through
the ferrite as if the permeabilityis close to that of free space. Over all frequencies we
have v p <v c and v g <v c . In contrast, an RHCP wave excites the electrons in the ferrite
and a resonance occurs at ω = ω 0 . For all frequencies below ω 0 we have v p <v c and
v g <v c and both v p and v g reduce to zero as ω → ω 0 . Because the ferrite is lossless,
frequencies between ω = ω 0 and ω = ω 0 + ω M result in β being purelyimaginaryand
thus the wave being evanescent. We thus call the frequencyrange ω 0 <ω <ω 0 + ω M
a stopband; within this band the plane wave cannot transport energy. For frequencies
above ω 0 + ω M the RHCP wave propagates as if it is in a medium with permeabilityless
than that of free space. Here we have v p >v c and v g <v c , with v p → v c and v g → v c as
ω →∞.

Faraday rotation. The solutions to the wave equation found above do not allow the
existence of linearlypolarized plane waves. However, bysuperposing LHCP and RHCP
waves we can obtain a wave with the appearance of linear polarization. That is, over
˜
any z-plane the electric field vector maybe written as E = K(E x0 ˆ x + E y0 ˆ y) where E x0
and E y0 are real (although K maybe complex). To see this let us examine

˜ ˜ + ˜ − E 0 − jβ + z E 0 − jβ − z
E = E + E = [ˆ x − j ˆ y]e + [ˆ x + j ˆ y]e
2 2

© 2001 by CRC Press LLC