Page 398 - Electromagnetics

2.5

2.0
β
ω/ω c 1.5 Light Line

1.0

0.5 α

0.0
0.0 0.5 1.0 1.5 2.0 2.5
β/ω v or α/ω v
c
c

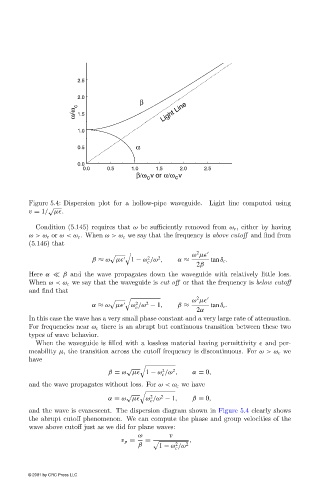
Figure 5.4: Dispersion plot for a hollow-pipe waveguide. Light line computed using
√
v = 1/ µ .
Condition (5.145) requires that ω be sufficiently removed from ω c , either by having
ω> ω c or ω< ω c . When ω> ω c we say that the frequency is above cutoff and find from
(5.146) that
ω µ
! 2

2
2
β ≈ ω µ 1 − ω /ω , α ≈ tan δ c .
c
2β
Here α β and the wave propagates down the waveguide with relatively little loss.
When ω< ω c we say that the waveguide is cut off or that the frequency is below cutoff
and find that
ω µ
! 2

2
2
α ≈ ω µ ω /ω − 1, β ≈ tan δ c .
c
2α
In this case the wave has a very small phase constant and a very large rate of attenuation.
For frequencies near ω c there is an abrupt but continuous transition between these two
types of wave behavior.
When the waveguide is filled with a lossless material having permittivity and per-
meability µ, the transition across the cutoff frequency is discontinuous. For ω> ω c we
have
√ !
2
2
β = ω µ 1 − ω /ω , α = 0,
c
and the wave propagates without loss. For ω< ω c we have
√ !
2
2
α = ω µ ω /ω − 1, β = 0,
c
and the wave is evanescent. The dispersion diagram shown in Figure 5.4 clearly shows
the abrupt cutoff phenomenon. We can compute the phase and group velocities of the
wave above cutoff just as we did for plane waves:
ω v
v p = = ,
β 1 − ω /ω 2
2
c
© 2001 by CRC Press LLC