Page 205 -

u=[1 5 3 2]
lengthu=norm(u) %length of vector u
unitu=u/(norm(u)) %unit vector parallel to u
lengthunitu=norm(unitu) %verify length of unit vector

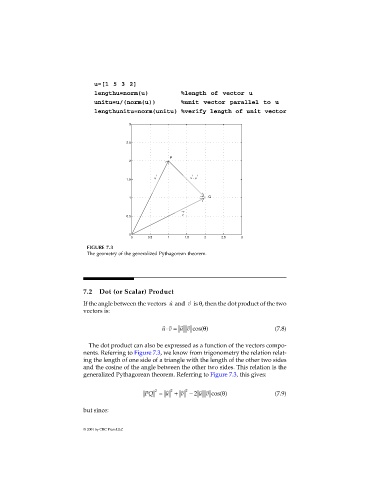
FIGURE 7.3
The geometry of the generalized Pythagorean theorem.

7.2 Dot (or Scalar) Product
r r
If the angle between the vectors and is θ, then the dot product of the twou v
vectors is:
r r r r
uv⋅= u v cos( )θ (7.8)

The dot product can also be expressed as a function of the vectors compo-
nents. Referring to Figure 7.3, we know from trigonometry the relation relat-
ing the length of one side of a triangle with the length of the other two sides
and the cosine of the angle between the other two sides. This relation is the
generalized Pythagorean theorem. Referring to Figure 7.3, this gives:

r r r r
2
2
PQ = u + v − 2 u v cos( )θ (7.9)
2
but since:

© 2001 by CRC Press LLC