Page 221 - Elements of Chemical Reaction Engineering 3rd Edition

Sec. 4.7 Unsteady-State Operation of Reactors 'I 93

(E4-1!.10)

The initial conditions are t = 0, CA = 0.05, C, = 0, Cc = C, = 0, and Vo = 5.
Equations (EX-11.2) through (E4-11.10) are easily solved with the aid of an
ODE solver such as POLYMATH (Table E4-11,l).

TABLE EX-11.1. POLYMATH PROGRAM
-
~
Equations Initial Values
-
d(cn)/d(t)=-Kxcaxcb-vOOXca/v 0.05
d( cb) /d( t) =-C*ca*cbtv@O*( cb0-cb) /v 0
d( CC) /d( t)=k*cn*cb-vOO*Lc/v 0
d( cd) /d( t) =k*ca*cb-v@O*cd/v 0
k.2.2
vOO=O. 05
cbO:O.O25
vO=5
caO=O .OS
rata=kxca*cb
v=votvoo* t
x=( raOtvO-ca*v) / (caO*vO)
to 5. 0, tF = 500
- -

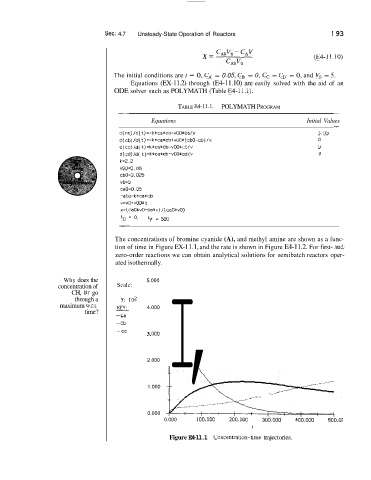
The concentrations of bromine cyanide (A), and methyl amine are shown as a func-
tion of time in Figure EX-1 1.1, and the rate is shown in Figure E4-11.2. For first- ilnd
zero-order reactions we can obtain analytical solutions for semibatch reactors oper-
ated isothermally.

Why does the 5.000
concentration of Scale:
CH, Br go
through a Y: 102
maximum w.r.t. KEY: 4.000
time? ~
-ca I,
-cb
-cc
3. DO0

2.000

1.000
.___..-
____.....
I
0.000
0.000
t
Figure E4-11.1 Concentration-time trajectories.