Page 486 - Elements of Chemical Reaction Engineering Ebook

Sec. 8.3 Nonisothermal Continuous-Flow Reactors 457
Computer Solution
We could have also solved this problem using POLYMATH or some other ODE
solver. The POLYMATH program using Equations (E8-6.1), (E8-6.1011, (E8-6.7),
(EF-6.11), (E8-6.12), and (E8-6.13) is shown in Table Ea-6.2. The graphical output is

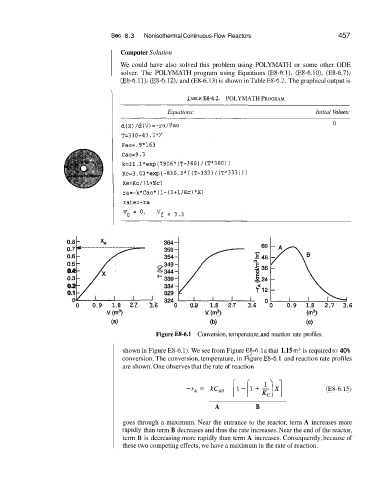
TAELE Ea-6.2. POLYMATH PROGRAM
Equations: Initial 'C'alues:

0.81 x,

0*5y,
0.3
0.4
0.2
0.1
0
0 0.9 1.8 2.7 3.6 0 0.91 1.8 2.7 3.6 0 0.9 1.8 2.7 3.6
v (m3) v (m3) on3)
(b) (c)
Figure E8-6.1 Conversion, temperature, and reaction rate profiles.

shown in Figure E8-6.1). We see from Figure E18-6. la that 1.15 m3 is required to 40%
conversion. The conversion, temperature, in Figure E8-6.1 and reaction rate profiles
are shown. One observes that the rate of reaction

(E8-6.15)

A B
goes through a maximum. Near the entrance to the reactor, term A increases more
rapiidly than term B decreases and thus the rate increases. Near the end of the reactor,
terrn B is decreasing more rapidly than term A increases. Consequently, because of
these two competing effects, we have a maximum in the rate of reaction.