Page 149 - Academic Press Encyclopedia of Physical Science and Technology 3rd Chemical Engineering

P1: LLL Final
Encyclopedia of Physical Science and Technology EN003H-565 June 13, 2001 20:37

Coherent Control of Chemical Reactions 211
s
with an analogous equation for P . The one- and three-
1
photon dipole operators are given by
D (1) =−µ · ε (9)
and
(1)
(1)
D |i
i|D | j
j|D (1)

(3)
D = , (10)
(E − ω 1 )(E − 2ω 1 )
i, j
where µ is the electronic dipole, ε is the electric field, and
the sum is over all states of the molecule.
For a single excitation path (i.e., one or three photons),
the only possibility for controlling the outcome of the re-
action is to select the excited eigenstate by varying E,asis
normally done in mode-selective processes. A completely
new form of control becomes possible, however, if both
excitation paths are simultaneously available. In that case,
the reaction probability is

2

s 3 ˆ (1) (3)
P = d k
g|D + D |E, S, k (11)
ˆ

We assume that the electric field is a plane wave linearly
polarized in the x direction,
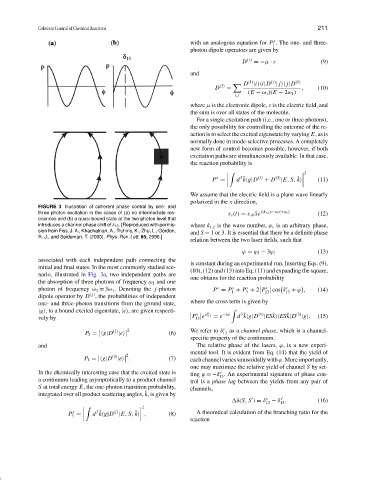
FIGURE 3 Illustration of coherent phase control by one- and
three-photon excitation in the cases of (a) no intermediate res- ε s (t) = ε s0 ˆ xe i(k s,z z−ω s t+ϕ s ) (12)
onances and (b) a quasi-bound state at the two-photon level that
introduces a channel phase shift of δ 13 . [Reproduced with permis- where k s,z is the wave number, ϕ s is an arbitrary phase,
sion from Fiss, J. A., Khachatrian, A., Truhins, K., Zhu, L., Gordon,
and S = 1 or 3. It is essential that there be a definite phase
R. J., and Seideman, T. (2000). Phys. Rev. Lett. 85, 2096.]
relation between the two laser fields, such that
(13)
ϕ = ϕ 3 − 3ϕ 1
associated with each independent path connecting the
is constant during an experimental run. Inserting Eqs. (9),
initial and final states. In the most commonly studied sce-
(10), (12) and (13) into Eq. (11) and expanding the square,
nario, illustrated in Fig. 3a, two independent paths are
one obtains for the reaction probability
the absorption of three photons of frequency ω 1 and one
s
s
s
s

photon of frequency ω 3 = 3ω 1 . Denoting the j-photon P = P + P + 2 P 13 cos δ + ϕ , (14)

1
s
13
3

( j)
dipole operator by D , the probabilities of independent
one- and three-photon transitions from the ground state, where the cross term is given by
|g , to a bound excited eigenstate, |e , are given respecti- s iδ s −iϕ 3 ˆ (1) (3)

ˆ
ˆ
vely by P 13 e 13 = e d k
g|D |ESk
ESk|D |g . (15)
2 s
(1) We refer to δ as a channel phase, which is a channel-
P 3 =
g|D |e (6) 13

specific property of the continuum.
and The relative phase of the lasers, ϕ, is a new experi-
mental tool. It is evident from Eq. (14) that the yield of
(3) 2
P 1 =
g|D |e . (7) eachchannelvariessinusoidallywithϕ.Moreimportantly,

one may maximize the relative yield of channel S by set-
In the chemically interesting case that the excited state is ting ϕ =−δ . An experimental signature of phase con-
s
13
a continuum leading asymptotically to a product channel trol is a phase lag between the yields from any pair of
S at total energy E, the one-photon transition probability, channels,
ˆ
integrated over all product scattering angles, k, is given by

s
s

δ(S, S ) = δ − δ . (16)
13
13
2

s 3 ˆ (i) A theoretical calculation of the branching ratio for the
P = d k
g|D |E, S, k , (8)
ˆ
3
reaction