Page 152 - Academic Press Encyclopedia of Physical Science and Technology 3rd Chemical Engineering

P1: LLL Final
Encyclopedia of Physical Science and Technology EN003H-565 June 13, 2001 20:37

214 Coherent Control of Chemical Reactions

and E res , , and are, respectively, the unperturbed
resonance center, the shift of the resonance, and its
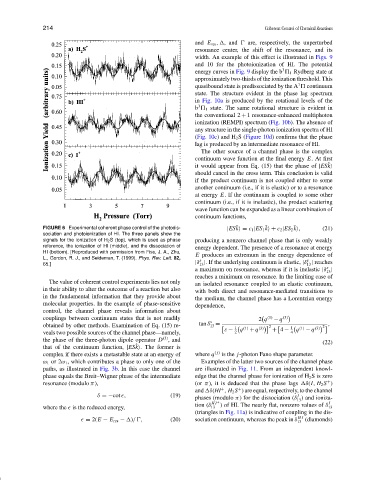
width. An example of this effect is illustrated in Figs. 9
and 10 for the photoionization of HI. The potential
3
energy curves in Fig. 9 display the b 1 Rydberg state at
approximately two-thirds of the ionization threshold. This
1
quasibound state is predissociated by the A continuum
state. The structure evident in the phase lag spectrum
in Fig. 10a is produced by the rotational levels of the
3
b 1 state. The same rotational structure is evident in
the conventional 2 + 1 resonance-enhanced multiphoton
ionization (REMPI) spectrum (Fig. 10b). The absence of
any structure in the single-photon ionization spectra of HI
(Fig. 10c) and H 2 S (Figure 10d) confirms that the phase
lag is produced by an intermediate resonance of HI.
The other source of a channel phase is the complex
continuum wave function at the final energy E. At first
ˆ
it would appear from Eq. (15) that the phase of |ESk
should cancel in the cross term. This conclusion is valid
if the product continuum is not coupled either to some
another continuum (i.e., if it is elastic) or to a resonance
at energy E. If the continuum is coupled to some other
continuum (i.e., if it is inelastic), the product scattering
wave function can be expanded as a linear combination of
continuum functions,

ˆ
ˆ
ˆ
FIGURE 6 Experimental coherent phase control of the photodis- |ESk = c 1 |ES 1 k + c 2 |ES 2 k , (21)
sociation and photoionization of HI. The three panels show the
signals for the ionization of H 2 S (top), which is used as phase producing a nonzero channel phase that is only weakly
reference, the ionization of HI (middle), and the dissociation of
energy dependent. The presence of a resonance at energy
HI (bottom). [Reproduced with permission from Fiss, J. A., Zhu,
L., Gordon, R. J., and Seideman, T. (1999). Phys. Rev. Lett. 82, E produces an extremum in the energy dependence of
s
s
65.] |δ |. If the underlying continuum is elastic, |δ | reaches
13
13
s
a maximum on resonance, whereas if it is inelastic |δ |
13
reaches a minimum on resonance. In the limiting case of
The value of coherent control experiments lies not only an isolated resonance coupled to an elastic continuum,
in their ability to alter the outcome of a reaction but also with both direct and resonance-mediated transitions to
in the fundamental information that they provide about the medium, the channel phase has a Lorentzian energy
molecular properties. In the example of phase-sensitive dependence,
control, the channel phase reveals information about
couplings between continuum states that is not readily 2 q (1) − q (3)

s
obtained by other methods. Examination of Eq. (15) re- tan δ = 1 2 1 ,
13
2
ε − q (1) + q (3) + 4 − q (1) − q (3)
veals two possible sources of the channel phase—namely, 2 4
(3)
the phase of the three-photon dipole operator D , and (22)
ˆ
that of the continuum function, |ESk . The former is
complex if there exists a metastable state at an energy of where q ( j) is the j-photon Fano shape parameter.
ω 1 or 2ω 1 , which contributes a phase to only one of the Examples of the latter two sources of the channel phase
paths, as illustrated in Fig. 3b. In this case the channel are illustrated in Fig. 11. From an independent knowl-
phase equals the Breit–Wigner phase of the intermediate edge that the channel phase for ionization of H 2 S is zero
+
resonance (modulo π), (or π), it is deduced that the phase lags δ(I, H 2 S )
and δ(HI , H 2 S ) are equal, respectively, to the channel
+
+
δ = −cot , (19) I
phases (modulo π) for the dissociation (δ ) and ioniza-
13
tion (δ HI + ) of HI. The nearly flat, nonzero values of δ I
where the is the reduced energy, 13 13
(triangles in Fig. 11a) is indicative of coupling in the dis-
= 2(E − E res − )/ , (20) sociation continuum, whereas the peak in δ HI (diamonds)
13