Page 247 - Academic Press Encyclopedia of Physical Science and Technology 3rd Chemical Engineering

P1: FYK/GJK P2: FJU Final Pages
Encyclopedia of Physical Science and Technology EN005B-205 June 15, 2001 20:24

154 Electrochemical Engineering

longer uniformly accessible to reactants. Instead, the reac-
tant concentration is highest at the leading edge and falls
as the reaction proceeds farther down the electrode. The
resulting current distribution tends to be skewed toward
the leading edge.
FIGURE 11 Plane parallel electrodes imbedded in insulating
walls. Fluid flows from right to left, and the reactant concentration V. SYSTEM DESIGN
tends to decrease in the direction of fluid flow as the electrochem-
ical reaction progresses.
A. Process Modeling
The modeling of electrochemical processes has evolved
current density. Therefore, in this system mass-transport
over the past 50 years to the point where complex prob-
limitations cause the current distribution to be more uni-
lems involving multiple reactions, temperature variations,
form. When the system is operating at the limiting current,
and physical property variations can be treated. Essen-
the current distribution is completely uniform.
tially all contemporary models require iterative computer
Channel flow between plane parallel electrodes is
techniques to simulate system behavior.
shown in Fig. 11. This geometry is similar to that of the
Several general techniques are used in the modeling of
disk in that an electrode and an insulator intersect in the
electrochemical systems. A method for reducing the ge-
same plane. Because of many geometric similarities, the
ometry to its basic configuration is called sectioning. In
general characteristics of the primary and secondary cur-
potential theory problems (primary and secondary current
rent distributions are similar. At the edges the local cur-
distributions) planes of symmetry can be replaced by in-
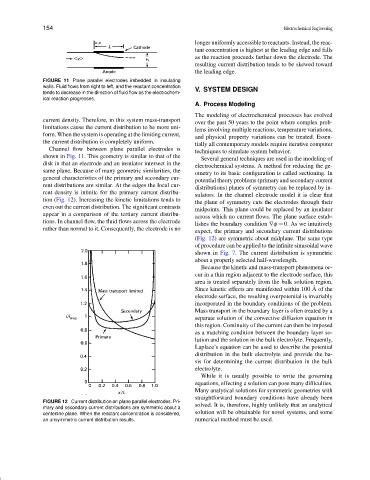
rent density is infinite for the primary current distribu-
sulators. In the channel electrode model it is clear that
tion (Fig. 12). Increasing the kinetic limitations tends to
the plane of symmetry cuts the electrodes through their
even out the current distribution. The significant contrasts midpoints. This plane could be replaced by an insulator
appear in a comparison of the tertiary current distribu-
across which no current flows. The plane surface estab-
tions. In channel flow, the fluid flows across the electrode
lishes the boundary condition ∇φ = 0. As we intuitively
rather than normal to it. Consequently, the electrode is no
expect, the primary and secondary current distributions
(Fig. 12) are symmetric about midplane. The same type
of procedure can be applied to the infinite sinusoidal wave
shown in Fig. 7. The current distribution is symmetric
about a properly selected half-wavelength.
Because the kinetic and mass-transport phenomena oc-
cur in a thin region adjacent to the electrode surface, this
area is treated separately from the bulk solution region.
˚
Since kinetic effects are manifested within 100 A of the
electrode surface, the resulting overpotential is invariably
incorporated in the boundary conditions of the problem.
Mass transport in the boundary layer is often treated by a
separate solution of the convective diffusion equation in
this region. Continuity of the current can then be imposed
as a matching condition between the boundary layer so-
lution and the solution in the bulk electrolyte. Frequently,
Laplace’s equation can be used to describe the potential
distribution in the bulk electrolyte and provide the ba-
sis for determining the current distribution in the bulk
electrolyte.
While it is usually possible to write the governing
equations, effecting a solution can pose many difficulties.
Many analytical solutions for symmetric geometries with
straightforward boundary conditions have already been
FIGURE 12 Current distribution on plane parallel electrodes. Pri-
mary and secondary current distributions are symmetric about a solved. It is, therefore, highly unlikely that an analytical
centerline plane. When the reactant concentration is considered, solution will be obtainable for novel systems, and some
an unsymmetric current distribution results. numerical method must be used.