Page 322 - Academic Press Encyclopedia of Physical Science and Technology 3rd Analytical Chemistry

P1: GNH Final Pages
Encyclopedia of Physical Science and Technology EN009N-447 July 19, 2001 23:3

Microwave Molecular Spectroscopy 839

(1)
E JKM = (J, K, M| | J, K, M)
−µ KM
=−µ (J, K, M| Zz |J, K, M) =
J(J + 1)
(106)
for the level J, K, M, where the matrix element is evalu-
ated in the symmetric rotor basis |J, K, M). The rotational
motion is like that of a top spinning about its symmetry
axis and also precessing about the vertical Z axis. The
frequency displacement is found by applying the selec-
tion rules J → J + 1, K → K, and M → M:
" #
2KM
(1)
ν ( M = 0) = (0.50344)µ ,
J(J + 1)(J + 2)
(107)
where J is the quantum number of the lower state of the
transition, and the factor 0.50344 has been introduced
so that ν is in MHz units if µ is in debye units and
is in volts per centimeter. Table XXIV gives the values
of the quantity in brackets for some low J values. For
example, with µ = 1 D and = 300 V/cm, we find for the
(J, K, M) = (1, 1, 1) → (2, 1, 1) transition that ν (1) =
50 MHz, a rather large splitting. Since K and M in
Eq. (107) can each take on values between J and −J,
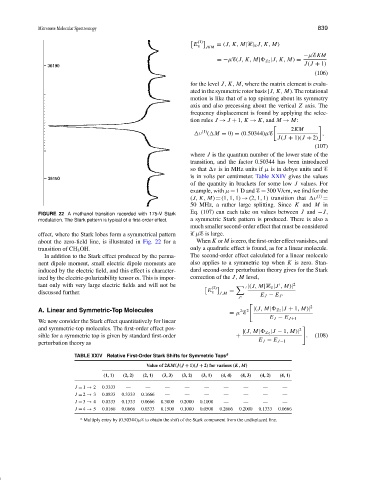
FIGURE 22 A methanol transition recorded with 175-V Stark
modulation. The Stark pattern is typical of a first-order effect. a symmetric Stark pattern is produced. There is also a
much smaller second-order effect that must be considered
effect, where the Stark lobes form a symmetrical pattern if µ is large.
about the zero-field line, is illustrated in Fig. 22 for a When K or M is zero, the first-order effect vanishes, and
transition of CH 3 OH. only a quadratic effect is found, as for a linear molecule.
In addition to the Stark effect produced by the perma- The second-order effect calculated for a linear molecule
nent dipole moment, small electric dipole moments are also applies to a symmetric top when K is zero. Stan-
induced by the electric field, and this effect is character- dard second-order perturbation theory gives for the Stark
ized by the electric-polarizability tensor α. This is impor- correction of the J, M level,
tant only with very large electric fields and will not be (2) |(J, M| |J , M)| 2

E =
discussed further. J,M
J E J − E J

2
A. Linear and Symmetric-Top Molecules = µ 2 |(J, M| Zz |J + 1, M)|
2
E J − E J+1
We now consider the Stark effect quantitatively for linear
and symmetric-top molecules. The first-order effect pos- 2
|(J, M| Zz |J − 1, M)|
sible for a symmetric top is given by standard first-order + . (108)
E J − E J−1
perturbation theory as
TABLE XXIV Relative First-Order Stark Shifts for Symmetric Tops a
Value of 2KM/J(J + + 1)(J + + 2) for various (K, M)
(1, 1) (2, 2) (2, 1) (3, 3) (3, 2) (3, 1) (4, 4) (4, 3) (4, 2) (4, 1)

J = 1 → 2 0.3333 — — — — — — — — —
J = 2 → 3 0.0833 0.3333 0.1666 — — — — — — —
J = 3 → 4 0.0333 0.1333 0.0666 0.3000 0.2000 0.1000 — — — —
J = 4 → 5 0.0166 0.0666 0.0333 0.1500 0.1000 0.0500 0.2666 0.2000 0.1333 0.0666
a
Multiply entry by (0.50344)µ to obtain the shift of the Stark component from the undisplaced line.