Page 58 - Subyek Encyclopedia - Encyclopedia of Separation Science

Sepsci*21*TSK*Venkatachala=BG
I / CHROMATOGRAPHY 53

between all components of interest in a mixture with-
in the shortest possible time. The resolution between
two peaks in a chromatogram depends on how well
the peak maxima are separated and how wide the two
peaks are. This can be expressed numerically by the
ratio of the separation of the two peak maxima
divided by the average peak widths at their base.
Baseline separation of the peaks is achieved at a res-
olution of about 1.5 but a value of 1.0, representing
about 94% peak separation, is taken as an adequate
goal for components that are difRcult to separate.
Resolution is also simply related to the properties of
the chromatographic system. For this purpose it is
convenient to consider a simple model of a three-
component mixture in which the optimum column
length is dictated by the number of theoretical plates
required to separate the two components that are
most difRcult to separate, and the total separation
time is dictated by the time required for the last peak
to elute from the column. The resolution of the two
peaks that are most difRcult to separate is then
related to the column variables by:

R S "( N/2) [( !1)/( #1)] k AV /(1#k AV ) [3]

where k AV is the average value of the retention factor
for the two peaks, or in an approximate form by:
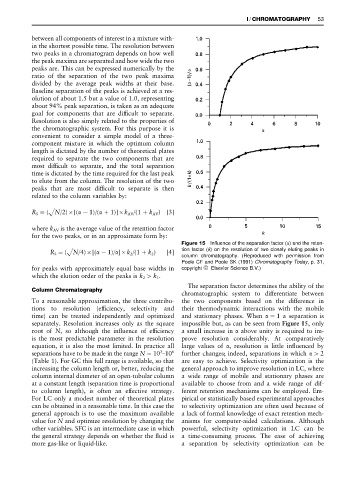
Figure 15 Influence of the separation factor ( ) and the reten-
R S "( N/4) [( !1)/ ] k 2 /(1#k 2 ) [4] tion factor (k) on the resolution of two closely eluting peaks in
column chromatography. (Reproduced with permission from
Poole CF and Poole SK (1991) Chromatography Today, p. 31,
for peaks with approximately equal base widths in copyright ^ Elsevier Science B.V.)
which the elution order of the peaks is k 2 'k 1 .
The separation factor determines the ability of the
Column Chromatography
chromatographic system to differentiate between
To a reasonable approximation, the three contribu- the two components based on the difference in
tions to resolution (efRciency, selectivity and their thermodynamic interactions with the mobile
time) can be treated independently and optimized and stationary phases. When "1 a separation is
separately. Resolution increases only as the square impossible but, as can be seen from Figure 15, only
root of N, so although the inSuence of efRciency a small increase in above unity is required to im-
is the most predictable parameter in the resolution prove resolution considerably. At comparatively
equation, it is also the most limited. In practice all large values of , resolution is little inSuenced by
3
separations have to be made in the range N"10 }10 6 further changes; indeed, separations in which '2
(Table 1). For GC this full range is available, so that are easy to achieve. Selectivity optimization is the
increasing the column length or, better, reducing the general approach to improve resolution in LC, where
column internal diameter of an open-tubular column a wide range of mobile and stationary phases are
at a constant length (separation time is proportional available to choose from and a wide range of dif-
to column length), is often an effective strategy. ferent retention mechanisms can be employed. Em-
For LC only a modest number of theoretical plates pirical or statistically based experimental approaches
can be obtained in a reasonable time. In this case the to selectivity optimization are often used because of
general approach is to use the maximum available a lack of formal knowledge of exact retention mech-
value for N and optimize resolution by changing the anisms for computer-aided calculations. Although
other variables. SFC is an intermediate case in which powerful, selectivity optimization in LC can be
the general strategy depends on whether the Suid is a time-consuming process. The ease of achieving
more gas-like or liquid-like. a separation by selectivity optimization can be