Page 98 - Engineering Digital Design

2.10 OTHER CODES 69

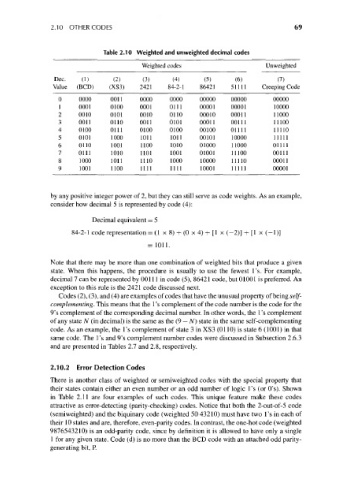
Table 2.10 Weighted and unweighted decimal codes

Weighted codes Unweighted
Dec. (1) (2) (3) (4) (5) (6) (7)
Value (BCD) (XS3) 2421 84-2-1 86421 51111 Creeping Code
0 0000 0011 0000 0000 00000 00000 00000
1 0001 0100 0001 0111 00001 00001 10000
2 0010 0101 0010 0110 00010 00011 11000
3 0011 0110 0011 0101 00011 00111 11100
4 0100 0111 0100 0100 00100 01111 11110
5 0101 1000 1011 1011 00101 10000 11111
6 0110 1001 1100 1010 01000 11000 01111
7 0111 1010 1101 1001 01001 11100 00111
8 1000 1011 1110 1000 10000 nno 00011
9 1001 1100 1111 mi 10001 11111 00001

by any positive integer power of 2, but they can still serve as code weights. As an example,
consider how decimal 5 is represented by code (4):
Decimal equivalent = 5
84-2-1 code representation = (1 x 8) + (0 x 4) + [1 x (-2)] + [1 x (-1)]

= 1011.

Note that there may be more than one combination of weighted bits that produce a given
state. When this happens, the procedure is usually to use the fewest I's. For example,
decimal 7 can be represented by 00111 in code (5), 86421 code, but 01001 is preferred. An
exception to this rule is the 2421 code discussed next.
Codes (2), (3), and (4) are examples of codes that have the unusual property of being self-
complementing. This means that the 1 's complement of the code number is the code for the
9's complement of the corresponding decimal number. In other words, the I's complement
of any state N (in decimal) is the same as the (9 — N) state in the same self-complementing
code. As an example, the I's complement of state 3 in XS3 (0110) is state 6 (1001) in that
same code. The I's and 9's complement number codes were discussed in Subsection 2.6.3
and are presented in Tables 2.7 and 2.8, respectively.

2.10.2 Error Detection Codes
There is another class of weighted or semiweighted codes with the special property that
their states contain either an even number or an odd number of logic I's (or O's). Shown
in Table 2.11 are four examples of such codes. This unique feature make these codes
attractive as error-detecting (parity-checking) codes. Notice that both the 2-out-of-5 code
(semiweighted) and the biquinary code (weighted 50 43210) must have two I's in each of
their 10 states and are, therefore, even-parity codes. In contrast, the one-hot code (weighted
9876543210) is an odd-parity code, since by definition it is allowed to have only a single
1 for any given state. Code (d) is no more than the BCD code with an attached odd parity-
generating bit, P.