Page 99 - Engineering Digital Design

70 CHAPTER 2 / NUMBER SYSTEMS, BINARY ARITHMETIC, AND CODES

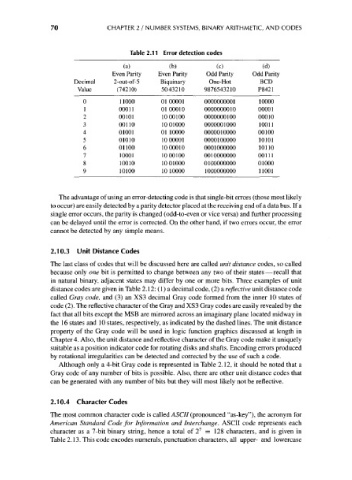
Table 2.11 Error detection codes
(a) (b) (c) (d)
Even Parity Even Parity Odd Parity Odd Parity
Decimal 2-out-of-5 Biquinary One-Hot BCD
Value (74210) 5043210 9876543210 P8421
0 11000 01 00001 0000000001 10000
1 00011 01 00010 0000000010 00001
2 00101 10 00100 0000000100 00010
3 00110 10 01000 0000001000 10011
4 01001 01 10000 0000010000 00100
5 01010 1000001 0000100000 10101
6 01100 1000010 0001000000 10110
7 10001 1000100 0010000000 00111
8 10010 1001000 0100000000 01000
9 10100 10 10000 1000000000 11001

The advantage of using an error-detecting code is that single-bit errors (those most likely
to occur) are easily detected by a parity detector placed at the receiving end of a data bus. If a
single error occurs, the parity is changed (odd-to-even or vice versa) and further processing
can be delayed until the error is corrected. On the other hand, if two errors occur, the error
cannot be detected by any simple means.

2.10.3 Unit Distance Codes
The last class of codes that will be discussed here are called unit distance codes, so called
because only one bit is permitted to change between any two of their states — recall that
in natural binary, adjacent states may differ by one or more bits. Three examples of unit
distance codes are given in Table 2.12: (1) a decimal code, (2) a reflective unit distance code
called Gray code, and (3) an XS3 decimal Gray code formed from the inner 10 states of
code (2). The reflective character of the Gray and XS3 Gray codes are easily revealed by the
fact that all bits except the MSB are mirrored across an imaginary plane located midway in
the 16 states and 10 states, respectively, as indicated by the dashed lines. The unit distance
property of the Gray code will be used in logic function graphics discussed at length in
Chapter 4. Also, the unit distance and reflective character of the Gray code make it uniquely
suitable as a position indicator code for rotating disks and shafts. Encoding errors produced
by rotational irregularities can be detected and corrected by the use of such a code.
Although only a 4-bit Gray code is represented in Table 2.12, it should be noted that a
Gray code of any number of bits is possible. Also, there are other unit distance codes that
can be generated with any number of bits but they will most likely not be reflective.

2.10.4 Character Codes
The most common character code is called ASCII (pronounced "as-key"), the acronym for
American Standard Code for Information and Interchange. ASCII code represents each
7
character as a 7-bit binary string, hence a total of 2 = 128 characters, and is given in
Table 2.13. This code encodes numerals, punctuation characters, all upper- and lowercase