Page 33 - Engineering Electromagnetics, 8th Edition

CHAPTER 1 Vector Analysis 15

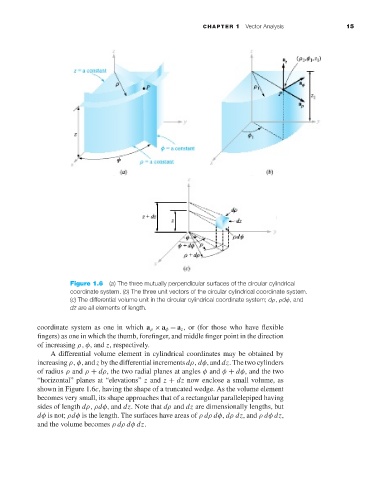
Figure 1.6 (a) The three mutually perpendicular surfaces of the circular cylindrical
coordinate system. (b) The three unit vectors of the circular cylindrical coordinate system.
(c) The differential volume unit in the circular cylindrical coordinate system; dρ, ρdφ, and
dz are all elements of length.

coordinate system as one in which a ρ × a φ = a z ,or (for those who have flexible
fingers) as one in which the thumb, forefinger, and middle finger point in the direction
of increasing ρ, φ, and z, respectively.
A differential volume element in cylindrical coordinates may be obtained by
increasing ρ, φ, and z by the differential increments dρ, dφ, and dz. The two cylinders
of radius ρ and ρ + dρ, the two radial planes at angles φ and φ + dφ, and the two
“horizontal” planes at “elevations” z and z + dz now enclose a small volume, as
shown in Figure 1.6c,having the shape of a truncated wedge. As the volume element
becomes very small, its shape approaches that of a rectangular parallelepiped having
sides of length dρ, ρdφ, and dz. Note that dρ and dz are dimensionally lengths, but
dφ is not; ρdφ is the length. The surfaces have areas of ρ dρ dφ, dρ dz, and ρ dφ dz,
and the volume becomes ρ dρ dφ dz.