Page 37 - Engineering Electromagnetics, 8th Edition

CHAPTER 1 Vector Analysis 19

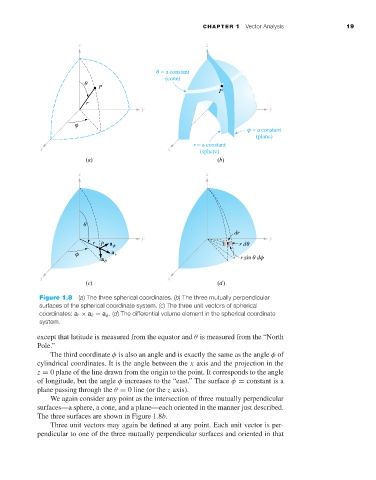
Figure 1.8 (a) The three spherical coordinates. (b) The three mutually perpendicular
surfaces of the spherical coordinate system. (c) The three unit vectors of spherical
coordinates: a r × a θ = a φ .(d) The differential volume element in the spherical coordinate
system.
except that latitude is measured from the equator and θ is measured from the “North
Pole.”
The third coordinate φ is also an angle and is exactly the same as the angle φ of
cylindrical coordinates. It is the angle between the x axis and the projection in the
z = 0 plane of the line drawn from the origin to the point. It corresponds to the angle
of longitude, but the angle φ increases to the “east.” The surface φ = constant is a
plane passing through the θ = 0 line (or the z axis).
We again consider any point as the intersection of three mutually perpendicular
surfaces—a sphere, a cone, and a plane—each oriented in the manner just described.
The three surfaces are shown in Figure 1.8b.
Three unit vectors may again be defined at any point. Each unit vector is per-
pendicular to one of the three mutually perpendicular surfaces and oriented in that