Page 344 - Engineering Electromagnetics, 8th Edition

326 ENGINEERING ELECTROMAGNETICS

On substituting (89) into (85), we obtain

V sT (z max ) = V 0 (1 +| |) (90)

As before, we may substitute (89) into the real instantaneous voltage (84). The effect
is to produce a maximum in the standing wave part, which then adds in-phase to the
running wave. The result is

V(z max , t) =±V 0 (1 +| |) cos(ωt + φ/2) (91)

where the plus and minus signs apply to positive and negative values of m in (89),
respectively. Again, the voltage oscillates through zero in time, with amplitude
V 0 (1 +| |).
Note that a voltage maximum is located at the load (z = 0) if φ = 0; moreover,
φ = 0 when is real and positive. This occurs for real Z L when Z L > Z 0 . Thus
there is a voltage maximum at the load when the load impedance is greater than Z 0
and both impedances are real. With φ = 0, maxima also occur at z max =−mπ/β =
−mλ/2. For a zero-load impedance, φ = π, and the maxima are found at z max =
−π/(2β), −3π/(2β), or z max =−λ/4, −3λ/4, and so forth.
The minima are separated by multiples of one half-wavelength (as are the
maxima), and for a zero load impedance, the first minimum occurs when −βz = 0,
or at the load. In general, a voltage minimum is found at z = 0 whenever φ = π;
this occurs if Z L < Z 0 where Z L is real. The general results are illustrated in
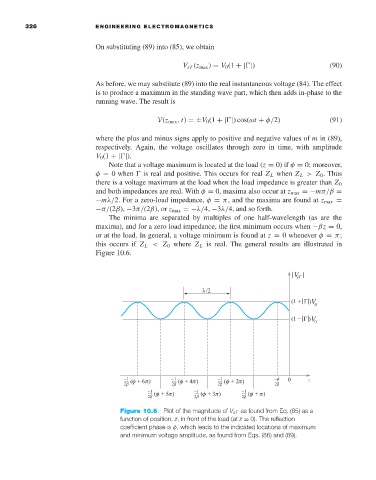
Figure 10.6.

V sT

V
0
V 0

Figure 10.6 Plot of the magnitude of V sT as found from Eq. (85) as a
function of position, z,infront of the load (at z = 0). The reflection
coefficient phase is φ, which leads to the indicated locations of maximum
and minimum voltage amplitude, as found from Eqs. (86) and (89).