Page 415 - Engineering Electromagnetics, 8th Edition

CHAPTER 11 The Uniform Plane Wave 397

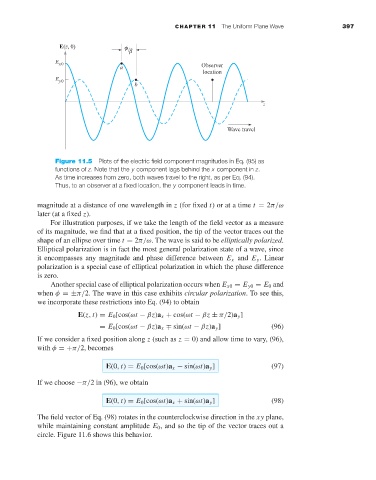
Figure 11.5 Plots of the electric field component magnitudes in Eq. (95) as
functions of z. Note that the y component lags behind the x component in z.
As time increases from zero, both waves travel to the right, as per Eq. (94).
Thus, to an observer at a fixed location, the y component leads in time.

magnitude at a distance of one wavelength in z (for fixed t)orata time t = 2π/ω
later (at a fixed z).
For illustration purposes, if we take the length of the field vector as a measure
of its magnitude, we find that at a fixed position, the tip of the vector traces out the
shape of an ellipse over time t = 2π/ω. The wave is said to be elliptically polarized.
Elliptical polarization is in fact the most general polarization state of a wave, since
it encompasses any magnitude and phase difference between E x and E y . Linear
polarization is a special case of elliptical polarization in which the phase difference
is zero.
Another special case of elliptical polarization occurs when E x0 = E y0 = E 0 and
when φ =±π/2. The wave in this case exhibits circular polarization.To see this,
we incorporate these restrictions into Eq. (94) to obtain
E(z, t) = E 0 [cos(ωt − βz)a x + cos(ωt − βz ± π/2)a y ]
= E 0 [cos(ωt − βz)a x ∓ sin(ωt − βz)a y ] (96)
If we consider a fixed position along z (such as z = 0) and allow time to vary, (96),
with φ =+π/2, becomes

E(0, t) = E 0 [cos(ωt)a x − sin(ωt)a y ] (97)

If we choose −π/2in (96), we obtain

E(0, t) = E 0 [cos(ωt)a x + sin(ωt)a y ] (98)

The field vector of Eq. (98) rotates in the counterclockwise direction in the xy plane,
while maintaining constant amplitude E 0 , and so the tip of the vector traces out a
circle. Figure 11.6 shows this behavior.