Page 56 - Engineering Electromagnetics, 8th Edition

38 ENGINEERING ELECTROMAGNETICS

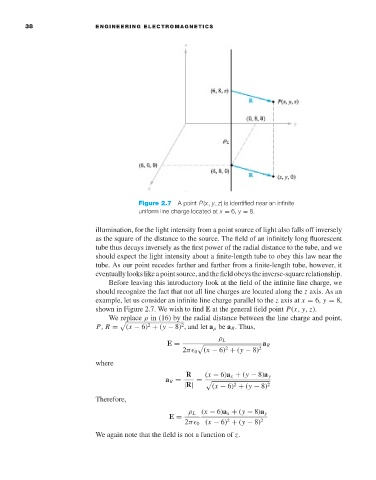
Figure 2.7 A point P(x, y, z)is identified near an infinite
uniform line charge located at x = 6, y = 8.

illumination, for the light intensity from a point source of light also falls off inversely
as the square of the distance to the source. The field of an infinitely long fluorescent
tube thus decays inversely as the first power of the radial distance to the tube, and we
should expect the light intensity about a finite-length tube to obey this law near the
tube. As our point recedes farther and farther from a finite-length tube, however, it
eventuallylookslikeapointsource,andthefieldobeystheinverse-squarerelationship.
Before leaving this introductory look at the field of the infinite line charge, we
should recognize the fact that not all line charges are located along the z axis. As an
example, let us consider an infinite line charge parallel to the z axis at x = 6, y = 8,
shown in Figure 2.7. We wish to find E at the general field point P(x, y, z).
We replace ρ in (16) by the radial distance between the line charge and point,
2
2

P, R = (x − 6) + (y − 8) , and let a ρ be a R . Thus,
ρ L
E = a R
2
2π 0 (x − 6) + (y − 8) 2
where
R (x − 6)a x + (y − 8)a y
a R = =
2
|R| (x − 6) + (y − 8) 2
Therefore,
ρ L (x − 6)a x + (y − 8)a y
E =
2
2π 0 (x − 6) + (y − 8) 2
We again note that the field is not a function of z.