Page 90 - Entrophy Analysis in Thermal Engineering Systems

82 Entropy Analysis in Thermal Engineering Systems

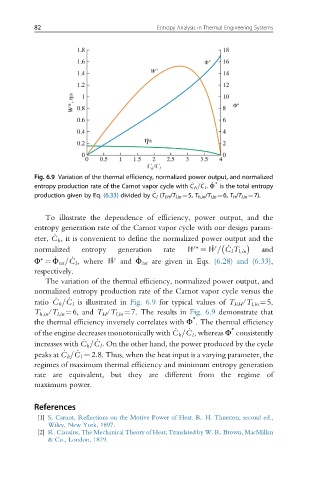
Fig. 6.9 Variation of the thermal efficiency, normalized power output, and normalized
∗
_
_
entropy production rate of the Carnot vapor cycle with C h =C l . _ Φ is the total entropy
_
production given by Eq. (6.33) divided by C l (T EH /T l,in ¼5, T h,in /T l,in ¼6, T H /T l,in ¼7).
To illustrate the dependence of efficiency, power output, and the
entropy generation rate of the Carnot vapor cycle with our design param-
_
eter, C h , it is convenient to define the normalized power output and the
_
normalized entropy generation rate W ∗ ¼ _ W = C l T l,in and
_
_
_
∗
Φ ¼ Φ tot =C l , where _ W and Φ tot are given in Eqs. (6.28) and (6.33),
respectively.
The variation of the thermal efficiency, normalized power output, and
normalized entropy production rate of the Carnot vapor cycle versus the
_
_
ratio C h =C l is illustrated in Fig. 6.9 for typical values of T EH /T l,in ¼5,
T h,in /T l,in ¼6, and T H /T l,in ¼7. The results in Fig. 6.9 demonstrate that
∗
the thermal efficiency inversely correlates with Φ . The thermal efficiency
∗
_
_
of the engine decreases monotonically with C h =C l , whereas Φ consistently
_
_
increases with C h =C l . On the other hand, the power produced by the cycle
_
_
peaks at C h =C l ¼ 2:8. Thus, when the heat input is a varying parameter, the
regimes of maximum thermal efficiency and minimum entropy generation
rate are equivalent, but they are different from the regime of
maximum power.
References
[1] S. Carnot, Reflections on the Motive Power of Heat. R. H. Thurston, second ed.,
Wiley, New York, 1897.
[2] R. Clausius, The Mechanical Theory of Heat, Translated by W. R. Brown, MacMillan
& Co., London, 1879.